目录
监督学习
监督学习的目标是学习一个未知的目标函数
学习的输入称为训练集,其中的数据是成对的,称为有标签样本
它满足
若是离散的,称为分类问题;若是连续的,称为拟合问题
学习的结果是目标函数的近似,记为,它取自一个预先设置的假设空间,其中包含了所有的可能函数
学习的过程是对假设空间施加约束的过程
学习效果的衡量
学习误差定义为
提示
学习误差=偏差+方差
其中偏差是不同训练集上预测结果偏离期望值的平均程度,方差是改变训练集导致的预测结果的变化。常用MSE衡量学习误差
相关信息
偏差和方差不能同时降低,因而需要根据实际的需要选择不同的权重对偏差和方差进行加权求和,称为偏差-方差折衷准则
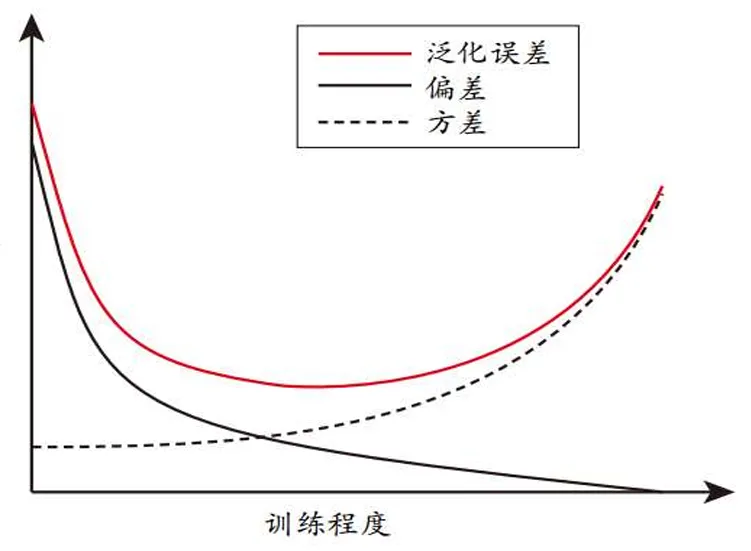
- 在训练不足时,学习器拟合能力不强,训练 数据的扰动不足以使学习器的拟合能力产生 显著变化,此时偏差主导泛化错误率
- 随着训练程度加深,学习器拟合能力逐渐增 强,训练数据的微小扰动导致学习器发生显 著变化,此时方差逐渐主导泛化错误率
- 训练充足后,学习器的拟合能力非常强,训 练数据的轻微扰动都会导致学习器的显著变 化,若训练数据自身非全局特性被学到则会 发生过拟合
模型评估
机器学习希望找到一个和未来的样例最佳拟合的假设。每个样例应当满足
- 每个样例出现的概率应当相等
- 每个样例出现与先前出现的样例无关,即是独立的
最佳拟合即希望错误率最小,即的比例。不过根据实际情况,机器学习中用损失函数代替错误率
损失函数定义为当真实情况为时,模型预测值为的效用损失,即输入为时,输出与的效用差值
对于回归任务常用的度量是均方误差MSE
也可以使用平均绝对值误差MAE
对于分类任务,错误率和精度是常用的性能度量
- 错误率:分错样本占样本总数的比率
- 精度(正确率):分对样本占样本总数的比率
统计真实标记和预测结果的组合可得到混淆矩阵

定义查准率和查全率
这是一对矛盾的指标,不可能都高。对样本进行分类时,模型给出样本为目标类别的概率。根据预测结果按正例可能性大小对样例进行排序,并逐个把样本作为正例进行预测,则可以得到查准率-查全率曲线,简称P-R曲线
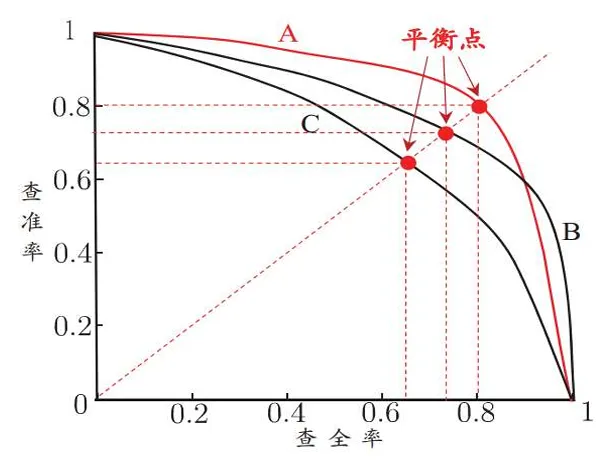
平衡点取为
对于P-R曲线有交叉的分类器可以用平衡点衡量性能高低。更常用的是F1度量
若对查准率和查全率的重视程度不同,应用
- :F1
- :重视查全率
- :重视查准率
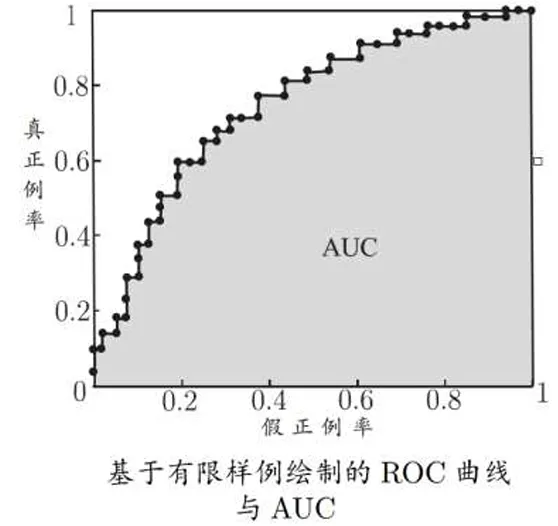
以假正例率为横轴,真正例率为纵轴,可以画出ROC曲线
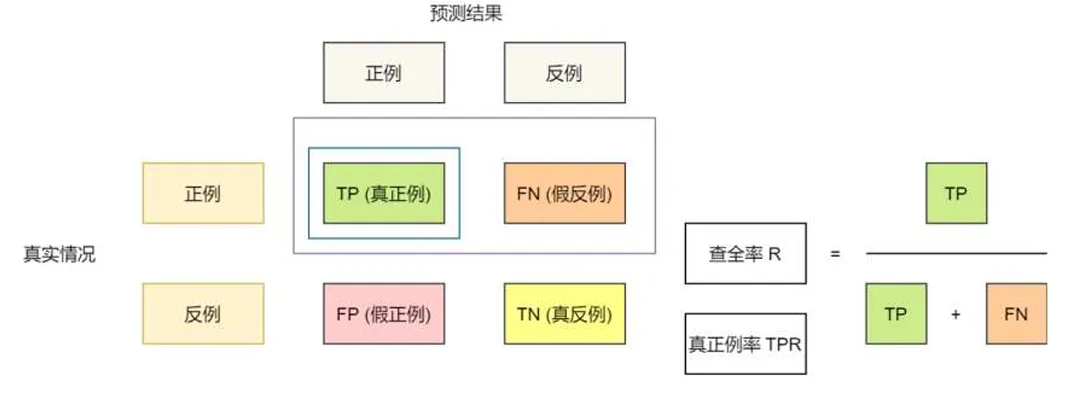
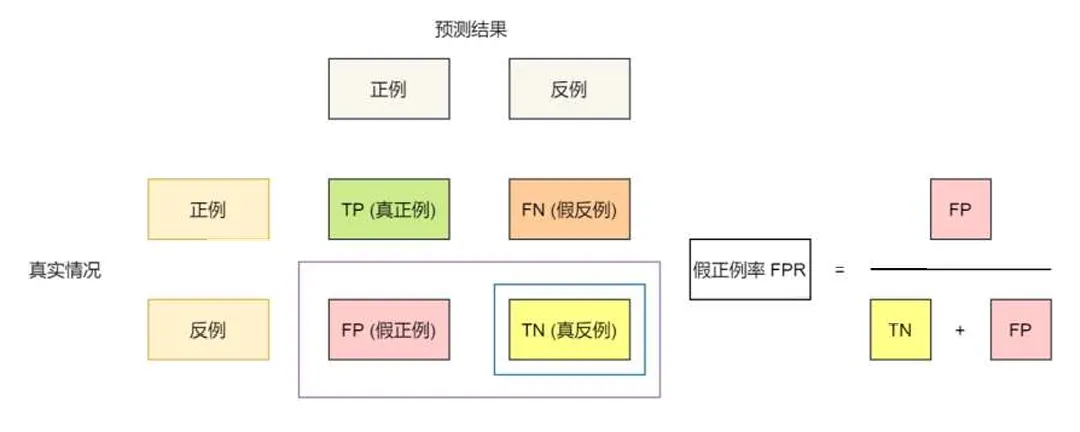
给定个整理和个反例,根据预测结果对样本排序,将分类阈值设为每个样本的预测值,记样本坐标
进行坐标映射
连接邻接点得到ROC图,面积称为AUC值
训练集、测试集、验证集
一般将样例分为两组
- 训练集(Training set):用于训练从而得到假设
- 测试集(Test set):用于评估假设的错误率
若模型需要超参数优化,或是评估不同的备选模型,还需要验证集 (Validation set)
直接将数据集划分为两个互斥集合的方式称为留出法。若样例数量不够,无法构成这三个数据集,可以采取如下的办法
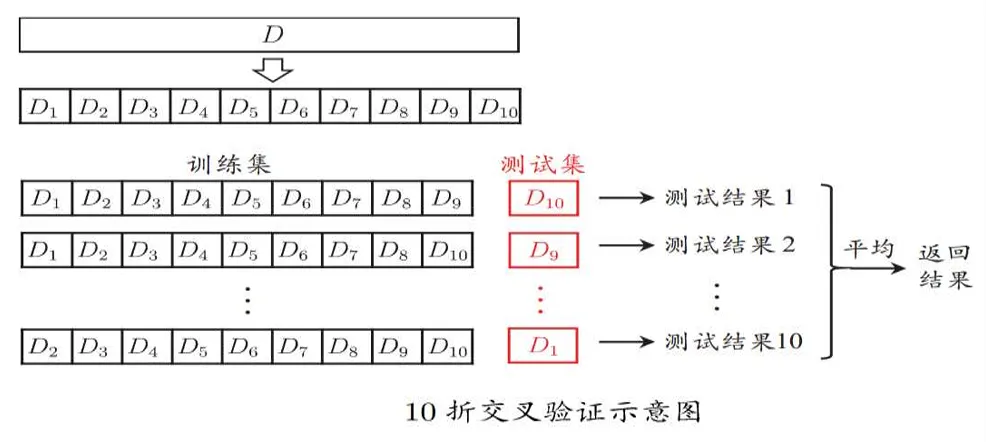
- k折交叉验证(k-fold cross-validation)的方法:每个样例都被作为训练数据和验证数据,但不同时提供
- 数据增强(Data Augmentation):使用少量数据通过先验知识产生更多的相似生成数据来扩展训练数据集
k折交叉验证即将数据集分层采样划分为k个大小相似的互斥子集,每次用子集的并作为训练集,余下一个子集作为测试集,最终返回k个测试结果的均值。常用k取10
对数据的划分方式可能存在多种,所以可以随机使用不同的划分方式重复p次,评估结果取为p次结果的均值,称为p次k折交叉验证
在数据集较小时,可以对数据集进行有放回采样。假定数据集大小为m,进行m次有放回采样得到训练集,会存在一些样本多次出现,一些样本不出现。对于一个样本,一次采样不被抽到的概率为
所以m次采样都不被抽到的概率为
令m趋于无穷得到
约摸三分之一的样本不会被抽到。这种方法称为自助法
泛化与过拟合
- 过拟合:创建的模型与训练数据过于匹配,以致于模型无法对新数据做出正确的预测
- 欠拟合:在训练集和测试集上的误差都很大
- 泛化能力:指模型对以前未见过的新数据做出正确预测的能力
本文作者:GBwater
本文链接:
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!