贝叶斯网络

贝叶斯网络是一张图，用节点表示随机变量，用一组有向边连接节点。如果一条边从 $X$ 指向 $Y$ ，则称 $X$ 是 $Y$ 的父节点

贝叶斯网络是一个无环图，对于每一个节点都有一张概率表，表示在其父亲给定的条件下节点的取值概率

可以简单地将边理解为因果关系

朴素贝叶斯

朴素贝叶斯的图由一个父节点和 $n$ 个子节点组成，在父节点的条件下各子节点独立

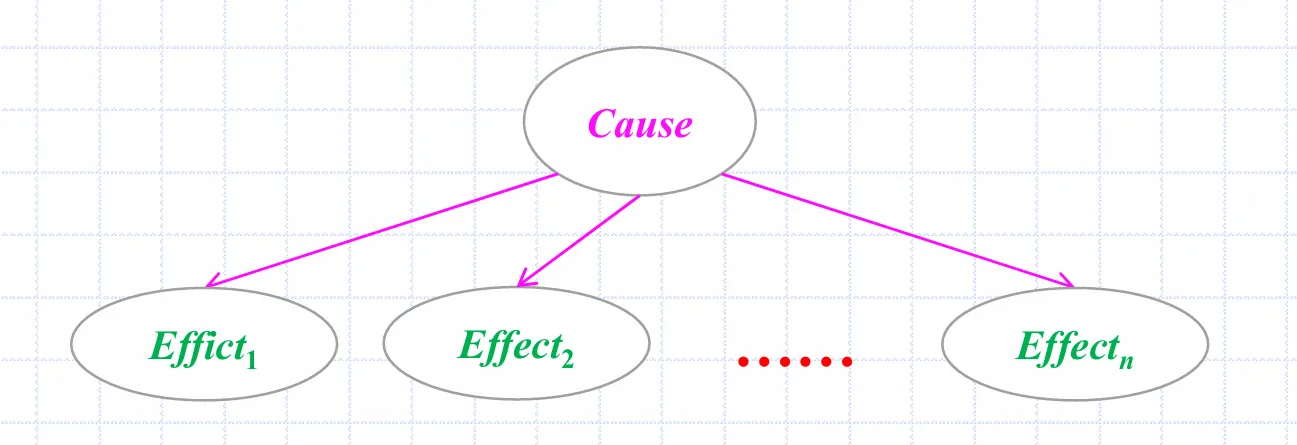
父节点没有父亲，它记录它自己的概率

P(Cause)

各个子节点记录在其父亲取各值的条件下取值的概率

P(Effect|Cause)

一般的贝叶斯网络

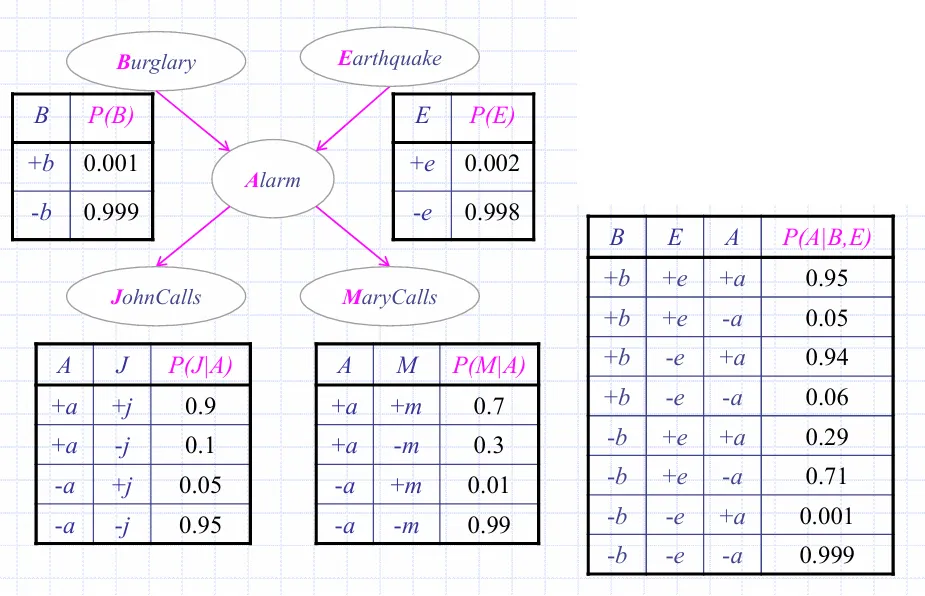
一个浅显的例子是

全局语义

如果需要查询 $n$ 个节点取值的联合概率

P(x_1,x_2,\cdots,x_n)

它们对应的变量节点记为

X_1,X_2,\cdots,X_n

由链式法则，应有

P(x_1,x_2,\cdots,x_n)=P(x_n|x_{n-1},x_{n-2,\cdots,x_1})P(x_{n-1},x_{n-2},\cdots,x_1)

将后面的联合概率进一步拆解，最终会得到

Note

P(x_1,x_2,\cdots,x_n)=P(x_n|x_{n-1},x_{n-2,\cdots,x_1})P(x_{n-1}|x_{n-2},\cdots,x_1)\cdots P(x_1)

如果这些节点存在一种顺序，满足

每个节点的父亲在前面的节点中

Parent(X_i)\subseteq {X_{i-1},X_{i-2},\cdots,X_1}

在给定父节点为条件的情况下，它与前面的其他节点是独立发的

P(X_i|X_{i-1},\cdots,X_N)=P(X_i|Parent(X_i))

那么联合概率就可以表示为乘积

Note

P(X_1,X_2,\cdots,x_n)=\prod_i P(X_i|Parent(X_i))

一个良好的贝叶斯网络应当能够满足这个条件

局部语义

注意到上一节“顺序”中的第二条

在给定父节点为条件的情况下，它与前面的其他节点是独立发的

$P(X_i|X_{i-1},\cdots,X_N)=P(X_i|Parent(X_i))$

它也可以表述为

给定一个节点的父节点, 那么它与其非后代节点条件独立
给定一个节点的父节点、子节点和子节点的父节点（马尔可夫毯）, 其条件独立与网络中其他所有节点

枚举推断

枚举推断即利用

P(X_1,X_2,\cdots,x_n)=\prod_i P(X_i|Parent(X_i))

需要枚举所有的可能事件。在上面的简单例子中

查询 $P(B|j,m)$

P(B|j,m)=\alpha\sum_e\sum_aP(B,j,m,e,a)=\alpha\sum_e\sum_aP(m|a)P(j|a)P(a|B,e)P(B)P(e)

计算时考虑 $B$ 的两种取值可能，它们具有相同的 $\alpha$ ，计算完成后它们之和应当为 $1$ ，做归一化得到系数 $\alpha$

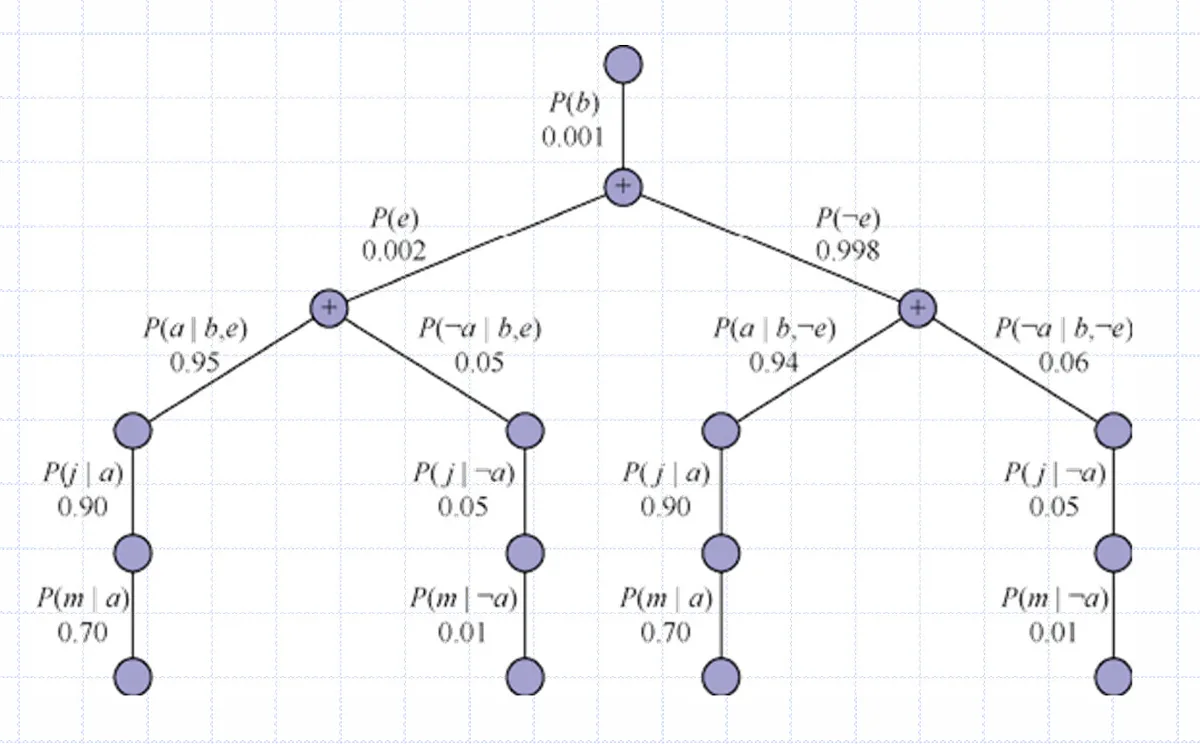
也可以采取深度优先的方式,从根节点（根本原因）出发做DFS，遍历所有情况。虽然也需要 $O(2^n)$ 的时间复杂度，但是空间复杂度变为了 $O(n)$

变量消元法

定义逐点乘积操作 $\times$ ，它将合并两个多元函数中的变量

f(X,Y)\times g(Y,Z)=h(X,Y,Z)

对于一组自变量的取值 $(x,y,z)$ ， $h(x,y,z)$ 定义为

h(x,y,z)=f(x,y)\cdot g(y,z)

再定义求和消元，它通过枚举某个自变量的所有取值并求和，进而消去它

\sum_X h(X,Y,Z)=\sum_xh(x,Y,Z)

对于布尔变量，自然有

\sum_X h(X,Y,Z)=h(x,Y,Z)+h(\neg x,Y,Z)

那么对于上面的计算

$P(B|j,m)=\alpha\sum_e\sum_aP(m|a)P(j|a)P(a|B,e)P(B)P(e)=\alpha P(B)\sum_eP(e)\sum_aP(a|B,e)P(m|a)P(j|a)$

它就可以写为

\alpha f_1(B)\times\sum_ef_2(e)\sum_af_3(a,B,e)\times f_4(a)\times f_5(a)

使用逐点乘积与求和消元即可完成计算