决策树

决策树适用于输入离散的情况。如餐厅等台问题

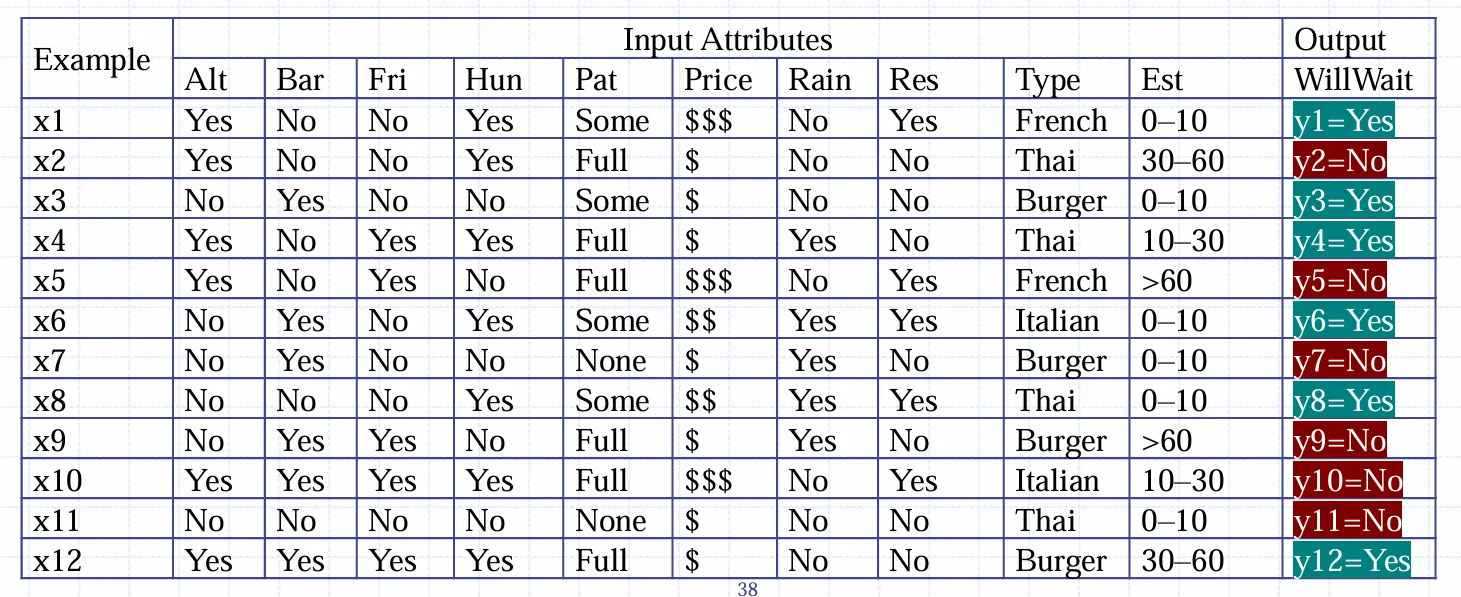
期望中应当构造这样一棵树，沿着树一路往下走最后完成决策过程

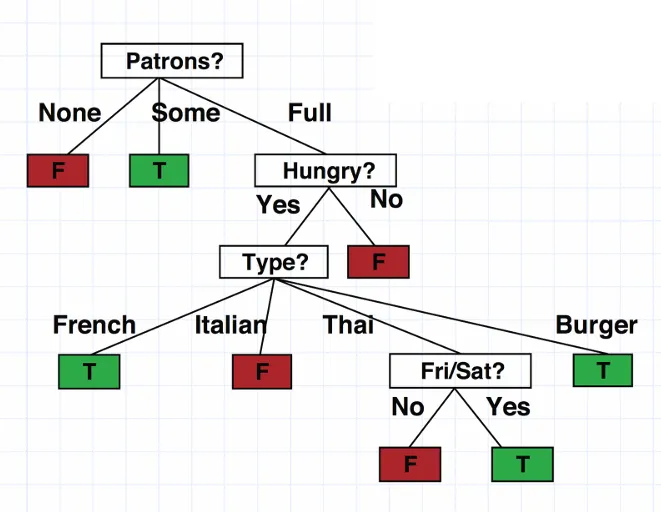
决策树的构造-ID3与C4.5

为了使得决策树的效率最高（树的高度应当尽量低），应当先决策重要的属性。“重要”的衡量标准是

Note

重要的属性能减小最大的不确定度

一个随机变量的不确定性由熵衡量

熵

H(V)=-\sum_kP(v_k)\log_2P(v_k)

为了衡量一个变量对不确定度的贡献，需要引入条件熵

条件熵

H(X|Y)=-\sum_{i,j}P(y_j)P(x_i|y_j)\log_2 P(x_i|y_j)

由此定义某个随机变量的信息增益，即获知 $Y$ 后减小的 $X$ 的不确定度

Gain(Y)=H(X)-H(X|Y)

每次选择信息增益最大的节点，由此构造高度最矮的决策树，这就是ID3算法

如果某属性的取值特别多，它的熵就会很高，这不利于决策树的构造，需要进行归一化，使得取值多和取值少的属性贡献度一致。C4.5算法中采用信息增益率代替信息增益做决策

IGR(E_1)=\dfrac{Gain(E_1)}{H(E_1)}=\dfrac{H(W)-H(W|E_1)}{H(E_1)}