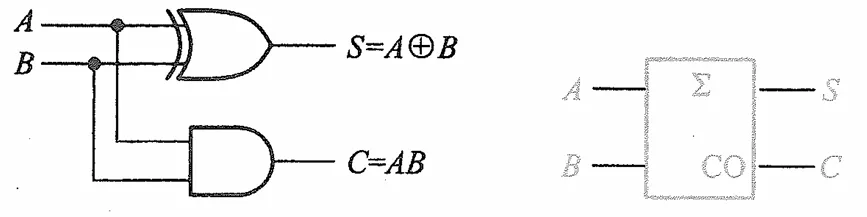半加器

半加器完成两个一位二进制数的加法，给出它们的加法结果和进位，不考虑更低位的进位

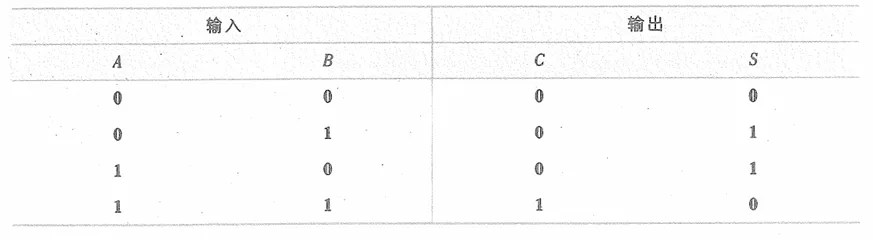
它的真值表是这样的，其中的 $C$ 是进位， $S$ 是该位的结果

可以写出其逻辑表达式

S=\bar{A}B+A\bar{B},\quad C=AB

它实际上就是异或和与，可以给出它的逻辑图

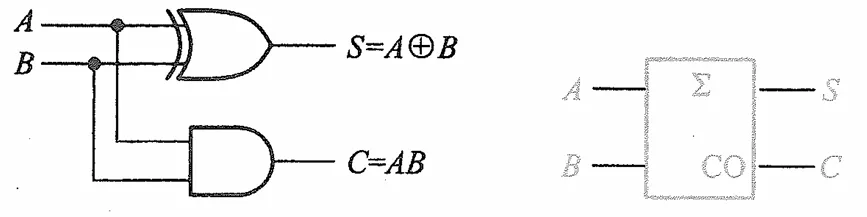
全加器

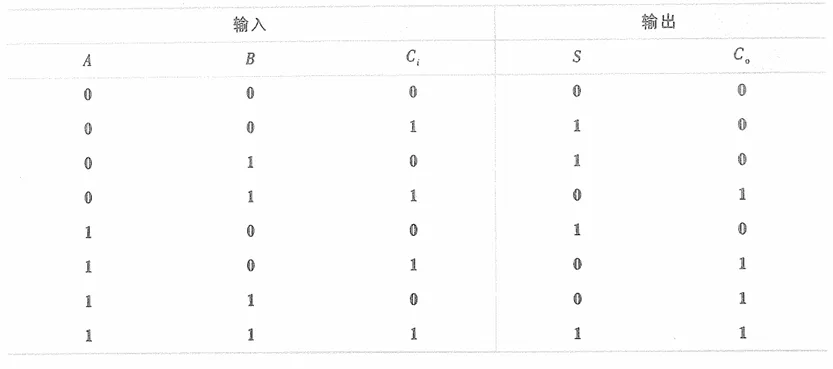
相比于半加器，全加器需要考虑更低位的进位，这可以用两个半加器实现，即先计算两个加数的加法，在计算结果与低位进位的加法，只要两个加法有一个出现了进位，进位的结果就是1（毕竟不可能都进位）。逻辑图就是这样子

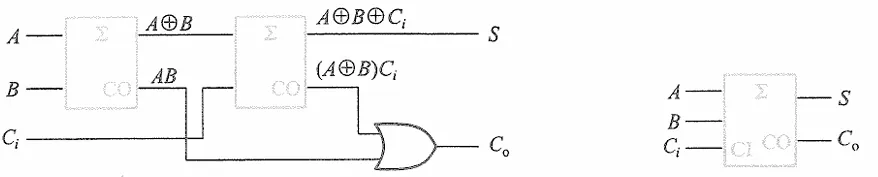
其真值表为

多位数加法可以采取串行的方式，将多个全加器串联起来

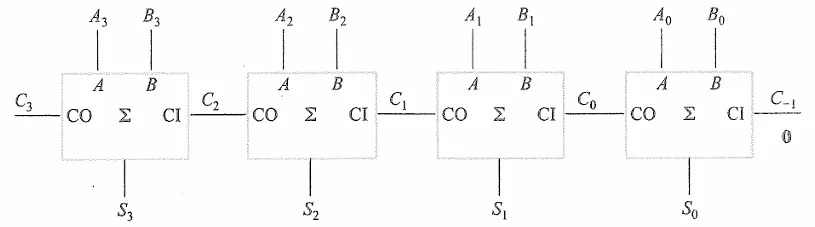
不过这样后面的加法需要等待前面完成计算后才能给出结果。如果想加快计算，需要采取超前进位的方式。鉴于全加器的逻辑表达式

S_i=A_i\oplus B_i\oplus C_{i-1},\quad C_i=A_iB_i+(A_i\oplus B_i)C_{i-1}

如果定义中间变量（就是半加器的计算结果）,它们与进位信号无关

G_i=A_iB_i,\quad P_i=A_i\oplus B_i

那么全加器的结果就写为了

S_i=P_i\oplus C_{i-1},\quad C_i=G_i+P_iC_{i-1}

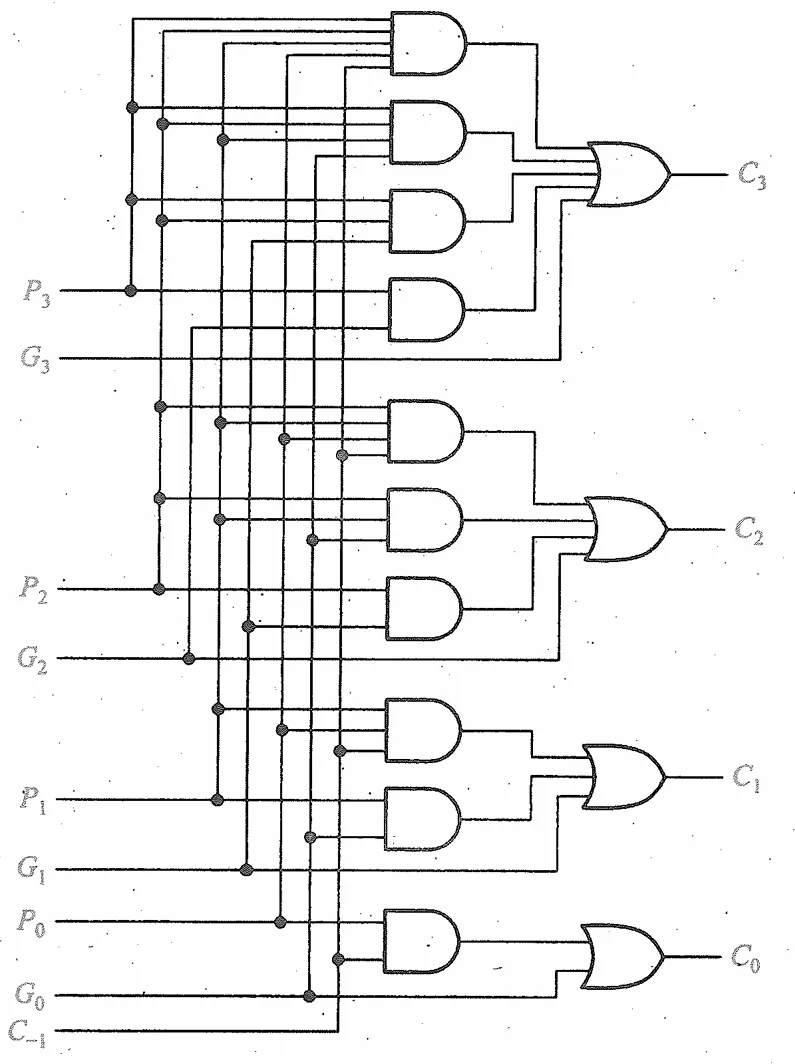
那么可以递归地消去所有的 $C$ ，将它们都用 $G_i,P_i$ 表示得到

\begin{aligned} C_0&=G_0+P_0C_{-1}\\ C_1&=G_1+P_1G_0+P_1P_0C_{-1}\\ C_2&=G_2+P_2G_1+P_2P_1G_0+P_2P_1P_0C_{-1}\\ C_3&=G_3+P_3G_2+P_3P_2G_1+P_3P_2P_1G_0+P_3P_2P_1P_0C_{-1} \end{aligned}

那么就可以实现超前进位产生电路

这样只需要再进行一次异或就能得到结果，得到超前进位加法器

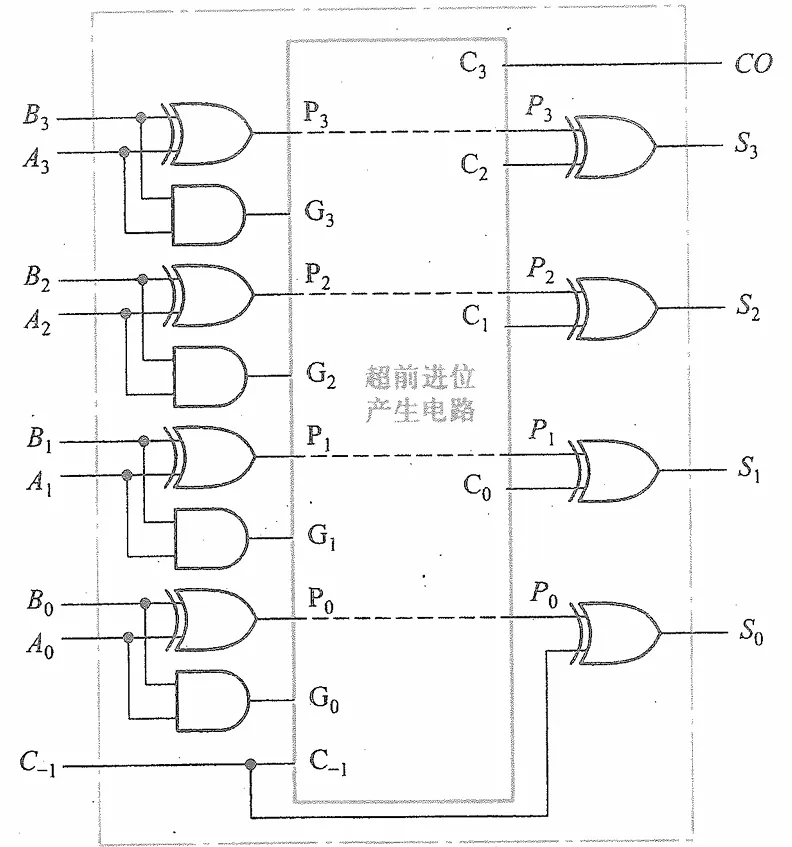
整个电路的延迟为4级门延迟。不过这样做的代价是电路变得复杂（要实现非常多的异或），因而可以将多个超前进位加法器串联起来（层次化串行进位扩展连接）

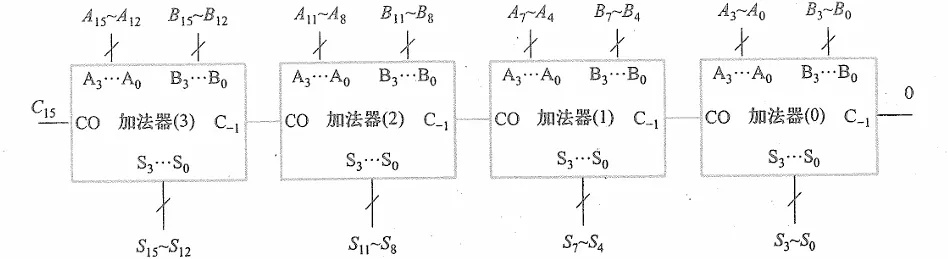
但是这样会慢，于是可以照猫画虎进行二级超前进位（层次化超前进位扩展连接）

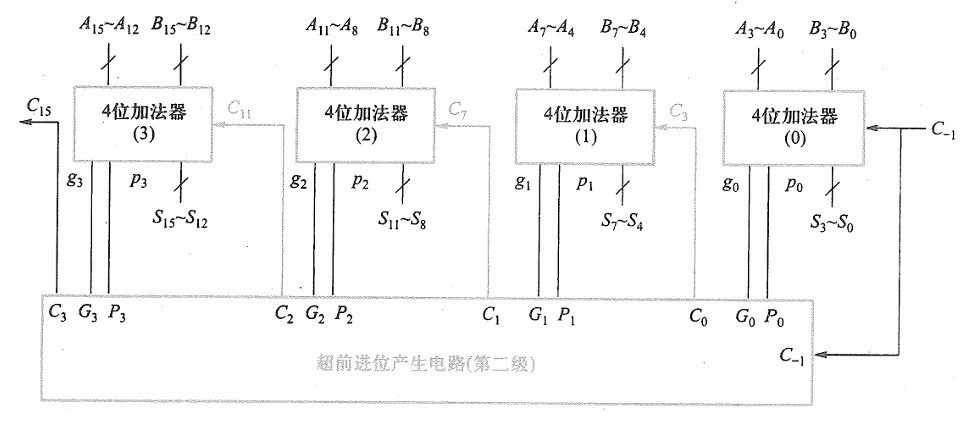
第二级超前进位产生电路与第一级相同，其中

g_i=P_3P_2P_1P_0,\quad g_i=G_3+P_3G_2+P_3P_2G_1+P_3P_2P_1G_0

上式中的 $G,P$ 是加法器内部的传输变量。这样完成16位数的加法只需要经过8级门延迟

可以使用补码实现减法。 $n$ 位二进制数的补码与原码的关系为

\text{补码}=2^n-\text{原码}

它可以用反码得到

\text{补码}=\text{反码}+1

这样就能实现减法

A-B=A+B_{\text{反}}+1-2^n

对于减去 $2^n$ 的运算，如果前面的加法正好进位了，进位就正好是 $2^n$ ，进位之外的结果就是正确的；如果没有进位，计算结果应是真实结果的补码，因为若是希望得到不考虑符号位的原码，则有

-\text{真实值的原码}=\text{计算结果}-2^n

这就需要一个求补电路将补码转换为原码，这可以用另一个加法器实现。总的来说，电路图为

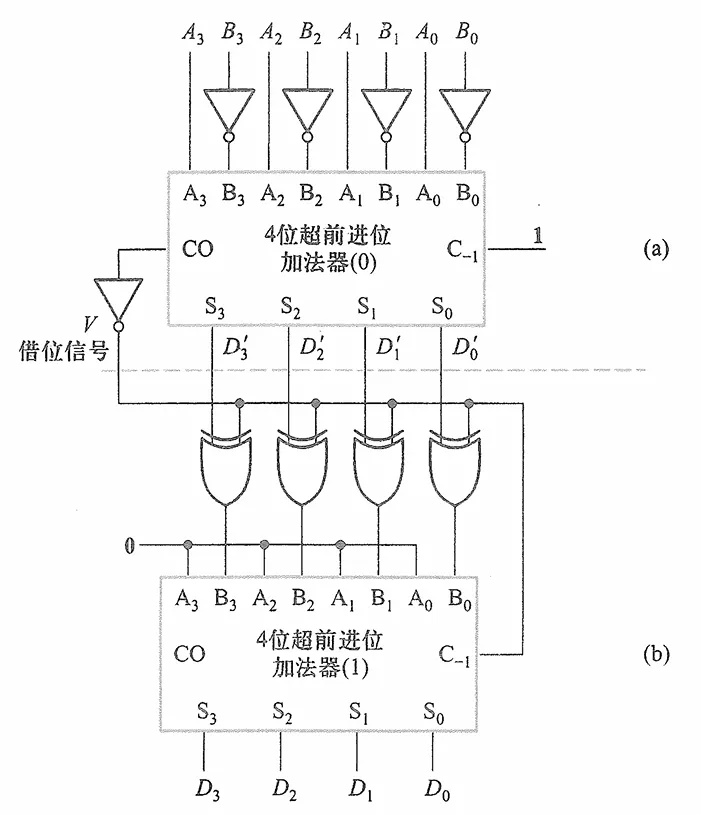
上半部分是减法电路，下半部分是求补电路，最后的输出是原码