神经网络与其前向传播

一个三层的简单神经网络可以如图画出

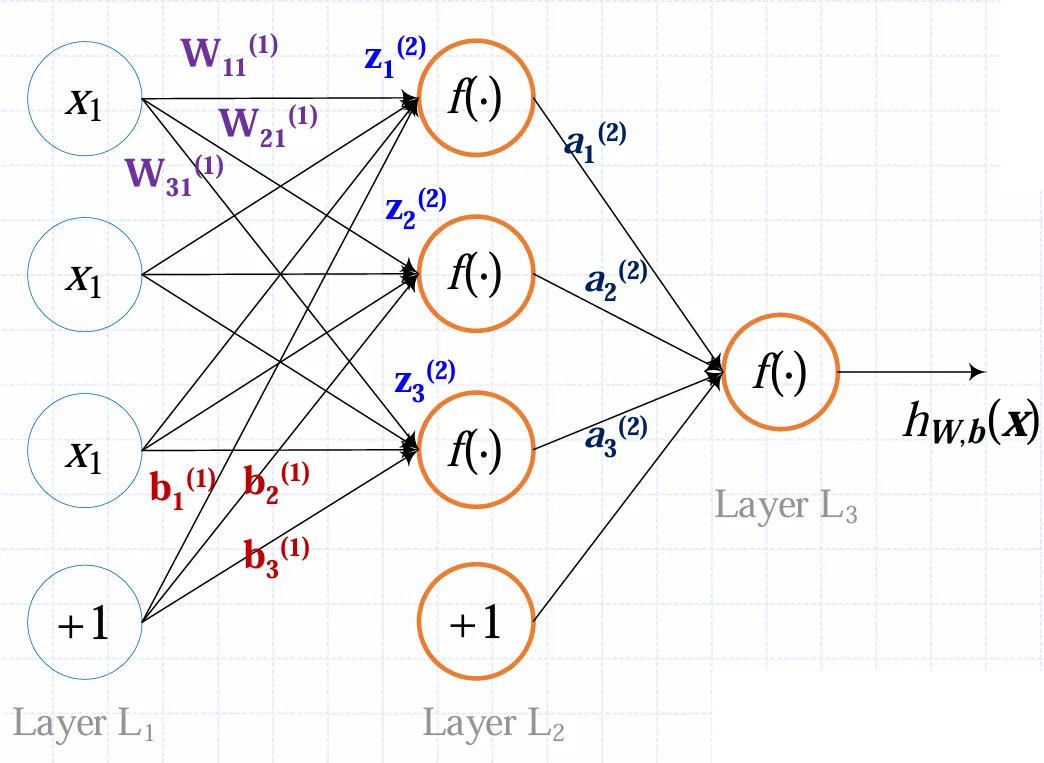
其中 $x_i$ 是输入， $+1$ 是偏置，各 $W$ 是权重，各 $b$ 是各个神经元的偏置，各 $z$ 是各个神经元的总输入，各 $a$ 是各神经元的输出，它们满足

z^{(2)}_i=\sum_j W_{ij}x_j+b^{(1)}_i

a^{(1)}_i=f(z_i^{(1)})

写成矢量形式会更加清晰

\bm{z}^{(l+1)}=\bm{W}^{(l)}\bm{a}^{(l)}+\bm{b}^{(l)}\quad \bm{a}^{(l+1)}=f(\bm{z}^{(l+1)})

实际上神经网络可以不止两层，输出神经元也可以不止一个。从输入一层一层地计算得到输出的过程就叫前向传播

神经网络的训练与误差反向传播

神经网络的训练即调整各个权重和偏置，使得代价函数最小。假定有很多个训练样本

(x^{(1)},y^{(1)}),\cdots,(x^{(m)},y^{(m)})

对于单个样本定义其代价函数为

J(W,b,x,y)=\dfrac12||h_{W,b}(x)-y||^2

总的代价函数除了各个样本的代价均值外，还要加上权重的惩罚项（Weight decay）

J(W,b)=\left[\dfrac1m\sum_{i=1}^m\left(\dfrac12||h_{w,b}(x^{(i)})-y^{(i)}||^2\right)\right]+\dfrac\lambda2\sum_{i,j,l}|W_{i,j}^{(l)}|^2

其中 $\lambda$ 是一个超参数，较大的 $\lambda$ 会使得训练倾向于减小权值。显然（好像也不显然） $J$ 并不是一个凸函数，理论上梯度下降法训练无法达到全局最优；不过实践中发现梯度下降法效果仍然不错

在更新参数时，也应遵循梯度下降法，按照代价函数的梯度更新参数

W_{ij}^{(l)}=W_{ij}^{(l)}-\alpha\dfrac{\partial}{\partial W_{ij}^{(l)}}J(W,b)

b^{(l)}=b^{(l)}-\alpha\dfrac{\partial}{\partial b^{(l)}}J(W,b)

鉴于

$z^{(2)}_i=\sum_j W_{ij}x_j+b^{(1)}_i$ $a^{(1)}_i=f(z_i^{(1)})$

只需要知道每个神经元的 $z$ 误差即可，定义感知误差，这是一个向量

\delta^{(l)}=\dfrac{\partial J(W,b)}{z^{(l)}}

利用链式法则可以得到

\delta^{(l)}=\dfrac{\partial a^{(l)}}{z^{(l)}}\cdot\dfrac{\partial z^{(l+1)}}{\partial a^{(l)}}\cdot\dfrac{\partial J(W,b)}{\partial z^{(l+1)}}=f'_l(z^{(l)})(W^{(l)})^T\delta^{(l+1)}

即得到了误差的递推关系。那么利用感知误差更新各参数

\dfrac{\partial}{\partial W_{ij}^{(l)}}J(W,b,x,y)=a_j^{(l)}\delta_i^{(l+1)}

\dfrac{\partial}{\partial b_i^{(l)}}J(W,b,x,y)=\delta_i^{(l+1)}

神经网络的每一层应当有

a_n=f(Wa_{n-1})

那么求其导有

\dfrac{\partial a_n}{\partial a_{n-1}}=f'\cdot W

那么当 $f'<1$ 时，梯度会在传播中越来越小；而 $W>1$ 时，梯度会越来越大。称之为梯度消失与梯度爆炸