双人零和博弈

双人零和博弈是两个玩家进行的零和博弈。零和博弈即

• 参与双方的效用相反，一个玩家的效用高就意为着另一个玩家的效用低
• 零和博弈是纯竞争而没有合作，不存在双赢

博弈双方可以采用同一效用值，一方使得效用最大，一方使得效用最小

可以给予双人零和博弈一个形式化的描述。将两个参与者分别称为MIN和MAX，MAX先移动，然后MIN移动，直到博弈结束

一个博弈中的状态需要有以下必要的属性：将要移动的玩家，可以采取的动作，是否终止。不妨给予定义

• $S_0$： 初始状态，即博弈开始时的状态
• To-Move(s)： 状态s下将要移动的玩家
• Action(s)： 状态s下全体合法移动的集合
• 转移模型Result(s,a)： 状态s下执行动作a产生的状态
• 中止测试Is-terminal(s)： 判断是否博弈结束
• 效用函数Utility(s)： 终止状态s下的效用函数

极小极大搜索(MiniMaxSearch)

极小极大算法适用于确定性的零和博弈，一方最小化结果，另一方最大化结果。假定所有参与者都最佳移动，极小极大算法期望中构造一棵状态空间搜索树，博弈双方轮流行动，如图

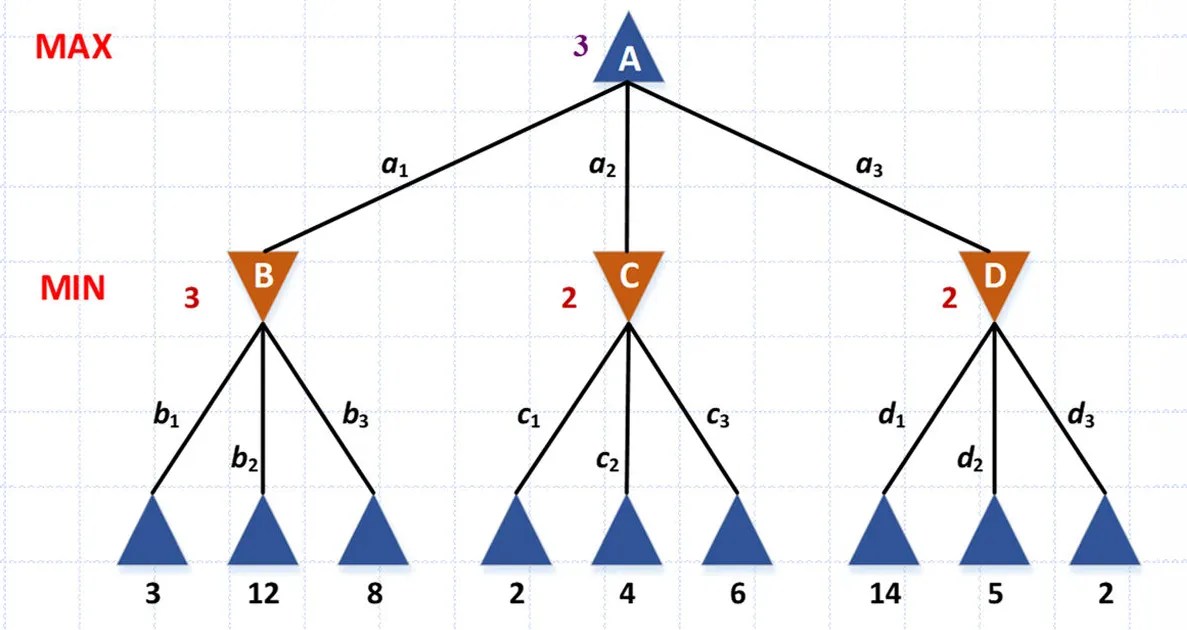
在博弈中，双方都选择对自己最有利的行为，即MAX选择效用最大的状态进行转移，MIN选择效用最小的状态进行转移。但是对于非终止状态无法定义效用，因而对于状态s定义极小极大值

即

对于MIN玩家而言，最佳的行动策略就是选取拥有最小MINMAX的状态；对于MAX玩家而言，最佳的行动策略就是选取拥有最大MINMAX的状态

极小极大搜索是对博弈树进行完整的深度优先搜索。记博弈树的最大深度为m，每个节点的合法行动数为b，那么它的时间复杂度是指数级的

由于是深度优先搜索，空间复杂度倒不大，为$O(bm)$。虽然它是完备的，但是需要的资源是非常难以满足的

$\alpha-\beta$剪枝

$\alpha-\beta$剪枝是对博弈树进行修剪，剪去了对结果没有影响的部分。$\alpha$剪枝是针对MAX玩家而言的，$\beta$剪枝是针对MIN玩家而言的

定义$\alpha$

如果在执行极大极小搜素时发现某个MAX将行动的节点其MINMAX小于$\alpha$，那么该节点以及它所有的兄弟节点都不需要考虑。这是因为MAX玩家应该尽可能选择高MINMAX值的节点所在分支，而不会允许MIN玩家逼自己选择较低MINMAX值的分支

再清晰一些的说法是，记该节点为n，它的父节点是MIN玩家做选择，MAX玩家是处于n还是n的兄弟是由MIN玩家决定的。MIN玩家一定会选择最小的MINMAX，轮到MAX玩家选择时，能确保的效用一定小于等于n节点的MINMAX，因而MAX玩家不会给MIN玩家选择的机会，即不会选择n所在的分支

这对于MIN玩家也是同理，定义$\beta$值

$\beta$剪枝策略是

$\alpha-\beta$剪枝的有效性依赖于节点的检查顺序。最坏的顺序是每次都考察最大的MAX和最小的MIN，无法减去任何的兄弟节点，最好顺序是考察最小的MAX和最大的MIN，可以剪去尽可能多的兄弟节点。在完美顺序下的时间复杂度为

启发式$\alpha-\beta$数搜索

在资源受限的情形下应使用深度受限搜索，即

• 截断测试(Cutoff-Test)代替终止测试
• 启发式评价函数EVAL代替效用函数Utility

评价函数评估非终止节点的分值，理想中应尽可能接近实际的MINMAX。由于深度受限，评价函数不可能完全与效用函数等同，会出现视野效应，即无法考虑搜索深度以外的情形

蒙特卡洛树搜索 (MCTS)

蒙特卡洛树搜索是基于概率模拟的结果构建启发式评价函数，一种常用的选择是Upper Confidence Bounder

其中

• $U(s)$是经过$s$节点所有模拟效用值之和
• $N(s)$为经过$s$节点的所有模拟次数
• $C$是一个常数，常取$\sqrt2$，用于平衡利用和探索

前一项$\dfrac{U(s)}{N(s)}$代表“经验”，即该节点的平均效用；后一项是考虑到其父节点的效用对它效用的修正，代表“探索”

随机博弈

随机博弈即一方选择动作后状态的转移并不确定，即存在“机会节点”

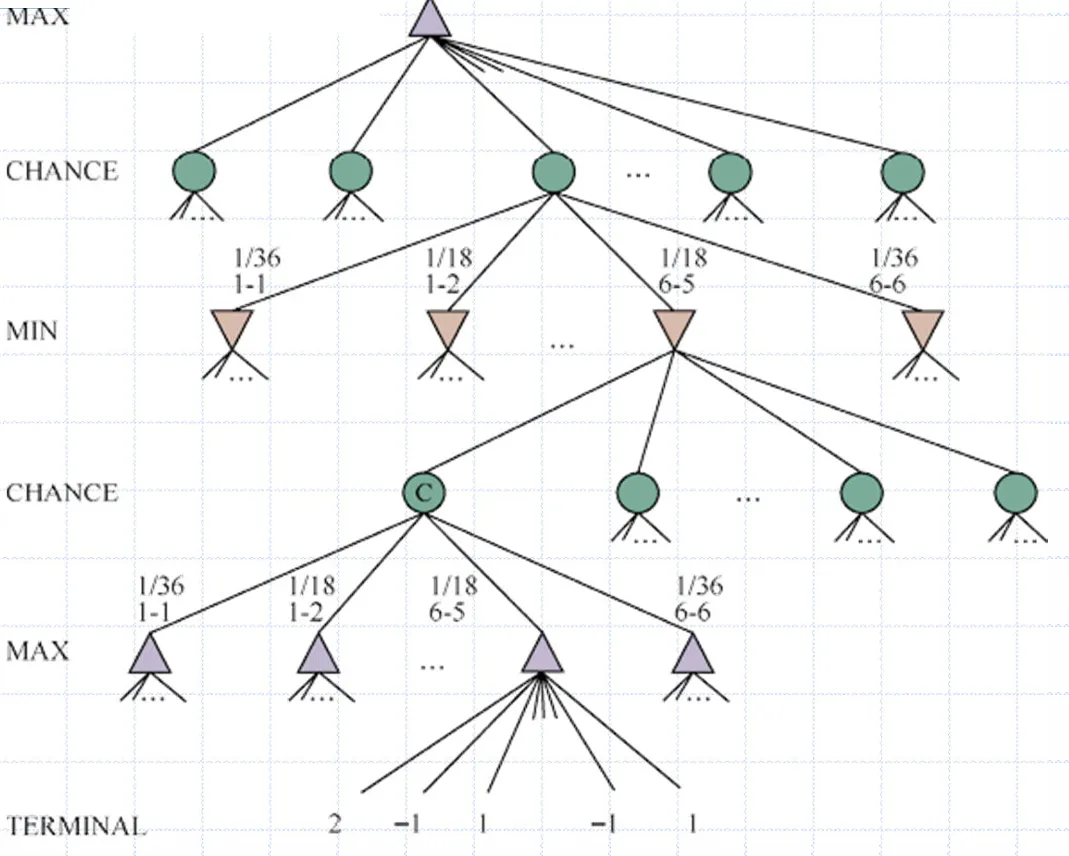
此时极小极大搜索中的MINMAX就可以变为期望MINMAX