感谢秦晓卫老师的指导！！

一般的搜索问题

搜索问题可以形式化定义为

• 状态空间：所有可能状态的集合
• 初始状态和目标状态
• 动作与动作代价
• 转移模型：描述动作如何决定状态的转移

一个动作序列称为路径，解是从初始状态到目标状态的一条路径

树搜索与搜索树

树搜索是一个逐步扩展的过程，搜索过程可以形象化地构成一棵搜索树。可以这样描述搜索过程

0. 初始化根节点为初始状态，根节点此时是唯一的叶子
1. 根据搜索策略挑选某一个叶子进行扩展，若没有可扩展的叶子则搜索失败
2. 若该叶子扩展出的节点中含有目标状态，则搜索成功返回结果；若没有，将这些节点加入搜索树中成为新的叶子，循环1

搜索树上的叶子称为边界节点，其他枝干称为内部区域；搜索树上的所有节点统一称为已达节点

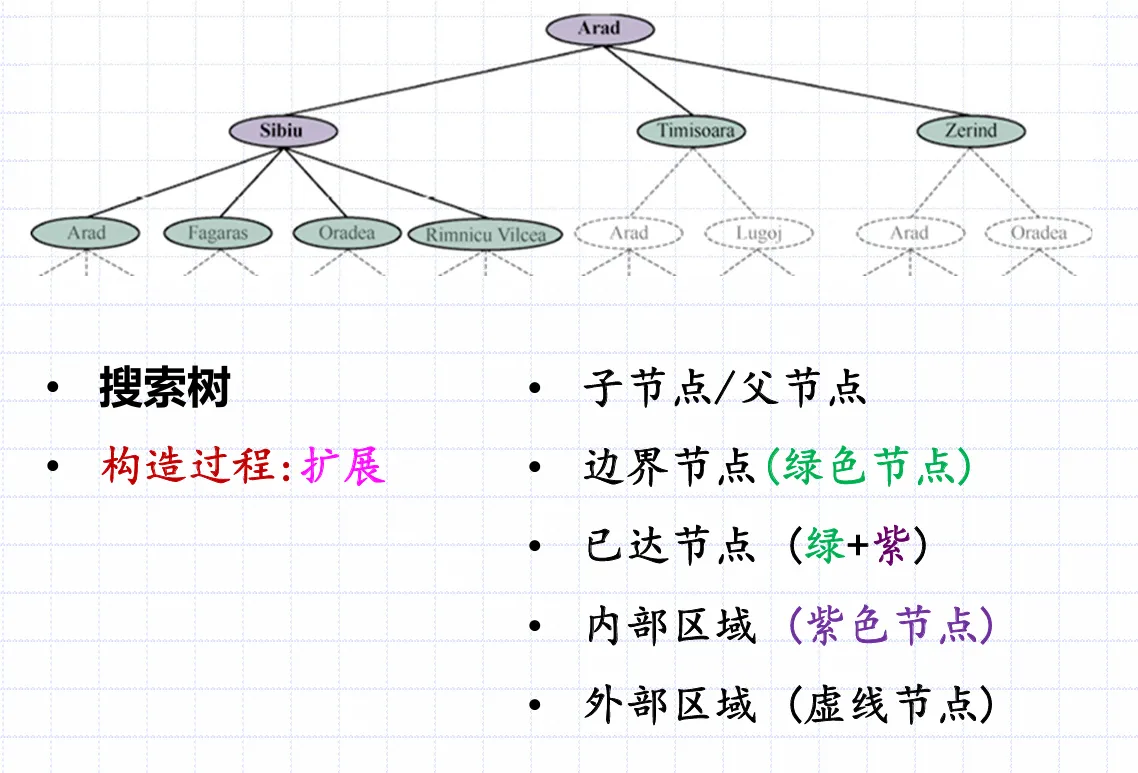
边界节点适宜使用优先队列维护

已达节点采用查找表的形式存储

无信息搜索：最佳优先搜索BFS（BestFirstSearch）

最佳优先搜索需要定义一个评价函数$f(n)$，不同的评价函数对应了不同的搜索算法。如评价函数可以为

• 节点$n$的深度
• 根节点到节点$n$的代价
• ...

若记 frontier 为边界节点集合，reached 为已达节点集合，那么最佳优先搜索可以描述如下

0. 初始化 frontier 为根，reached 为空
1. 从frontier中弹出使得$f(n)$最小的节点，扩展其子节点
2. 由子节点更新reached集合与路径代价，并将子节点添加进入frontier集合
3. 返回 1 循环直到frontier为空或是找到目标状态

图搜索与状态空间图

可以将状态空间画为图，状态用节点表示，状态的转移关系对应节点的输出弧。一个简单的状态空间图如下

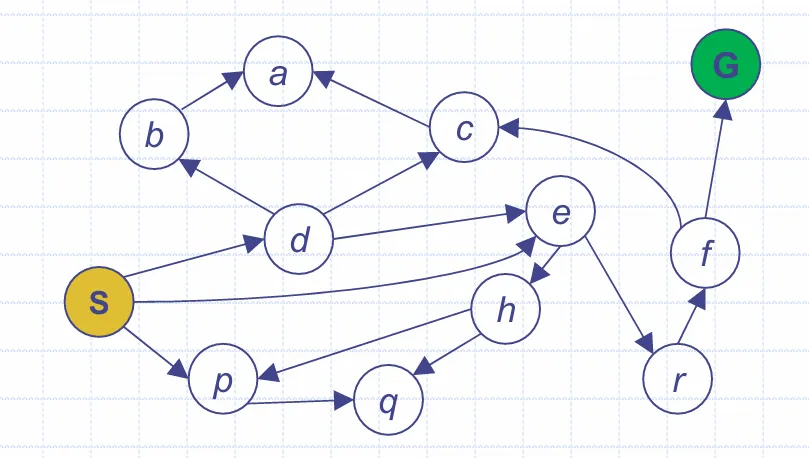
对于较复杂的状态转移关系，搜索树中会出现重复的节点，每个两个节点间存在多条 冗余路径