目录
如果不清楚数据中到底包含几类,则聚类算法可以分为层次聚类和密度聚类。层次聚类不断将两类合并为一类,形成一棵聚类树,然后划分聚类树得到类别;密度聚类则按密度扩张类别,不形成聚类树。层次聚类可以自动进行,不需要人为设置参数;而密度聚类需要给定密度阈值参数,并且对不同密度的簇聚类效果不好
将层次聚类与密度聚类相结合就能得到HDBSCAN算法,它通过空间变换使得适应不同密度的簇,并且引入稳定度的概念自动划分聚类树,并获得对噪声的良好抵抗效果
空间变换:核心距离与互达距离
进行空间变换的目的是适应不同密度的簇。对于一个数据点,给定参数k,它的核心距离定义为
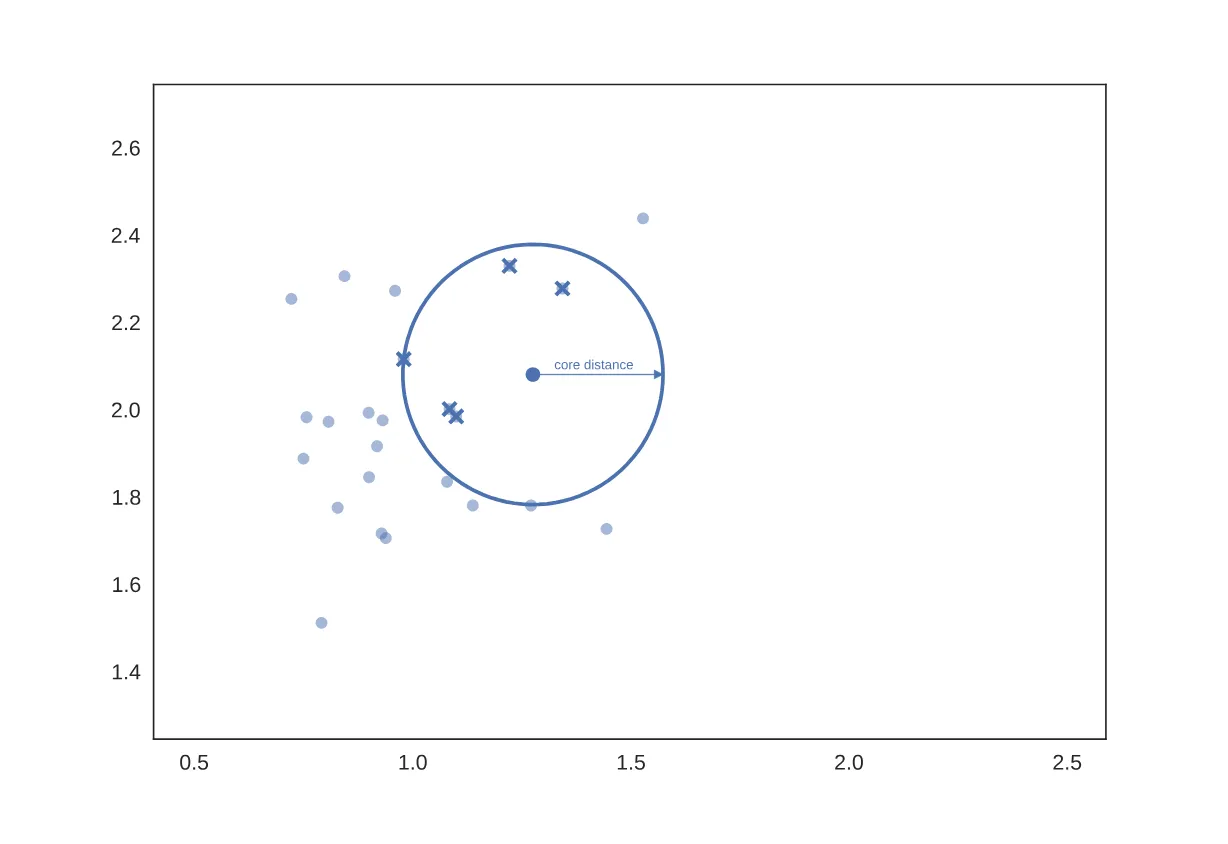
核心距离
一个样本点的核心距离是距离它最近的第k个样本点与它的距离
如果取,则核心距离的示意图如图(图源hdbscan.readthedocs.io)
进一步,得到每个样本点的距离之后,就可以对距离矩阵(每两个样本点之间的距离)做变换,得到互达距离矩阵
互达距离
两个样本点的互达距离是以下三者的最大值
- 它们之间的距离
- 一个样本点的核心距离
- 另一个样本点的核心距离
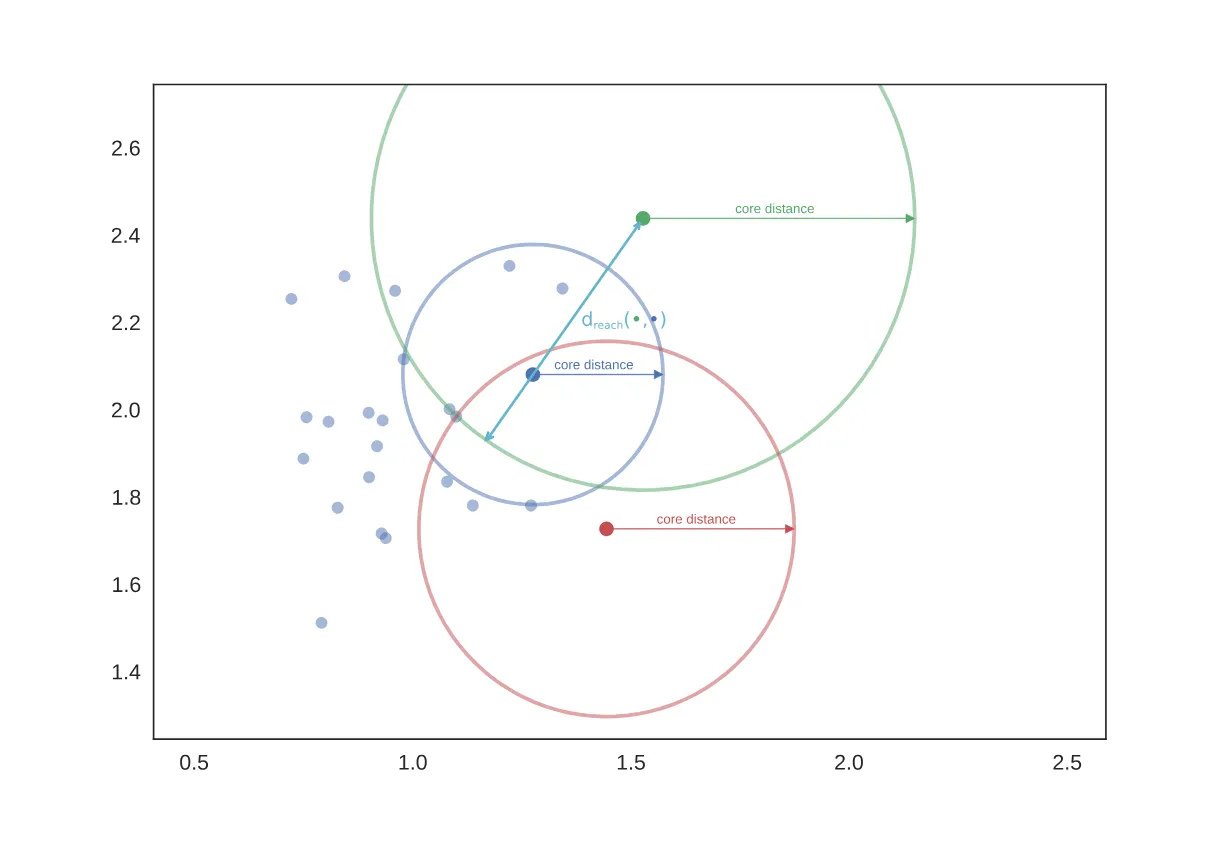
如果取,则互达距离的示意图如图(图源hdbscan.readthedocs.io)
这种情况下互达距离是其中一个样本点的核心距离
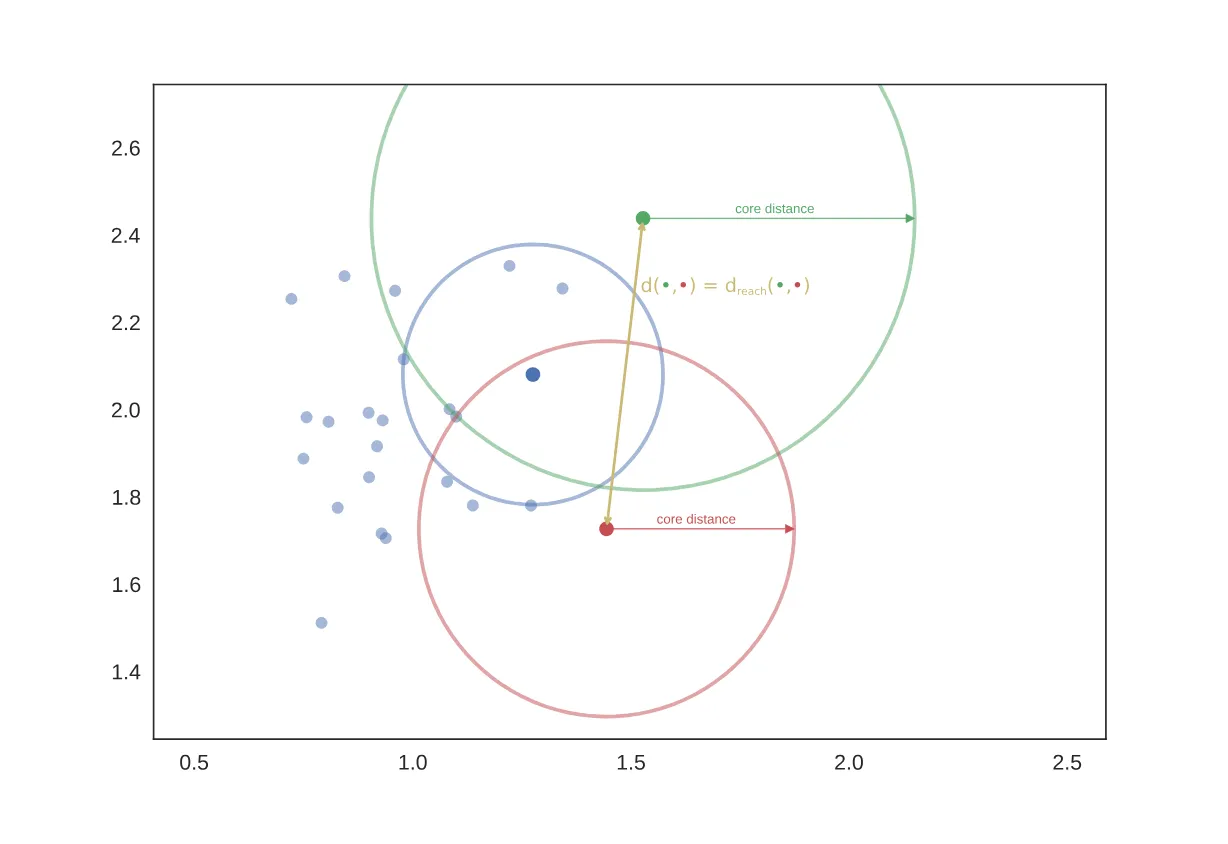
这种情况下互达距离是两个样本点的距离
构造最小生成树,进行层次聚类
假定有一个二维样本点分布是这样的(图源hdbscan.readthedocs.io)
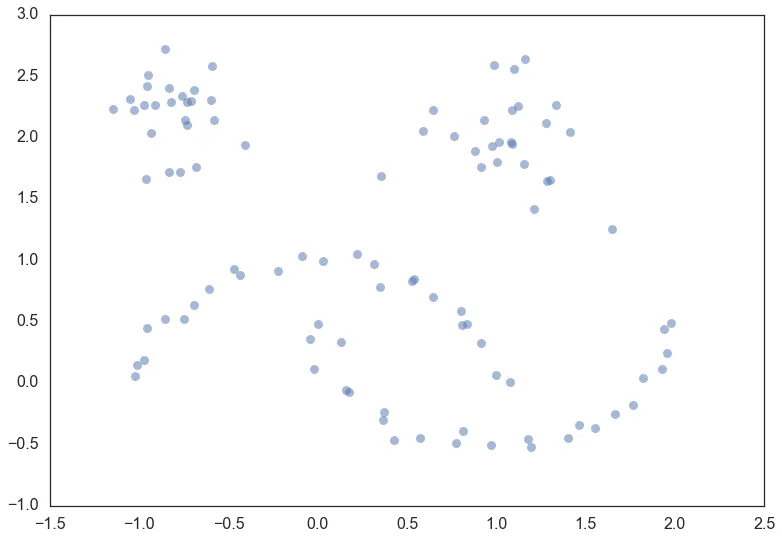
记样本点数目为,利用个互达距离作为边连接各个样本点形成一张图,在此图的基础上构造最小生成树。由于这是一个稠密图,利用Prim算法会取得较优的时间复杂度
构造得到的最小生成树如图(图源hdbscan.readthedocs.io)
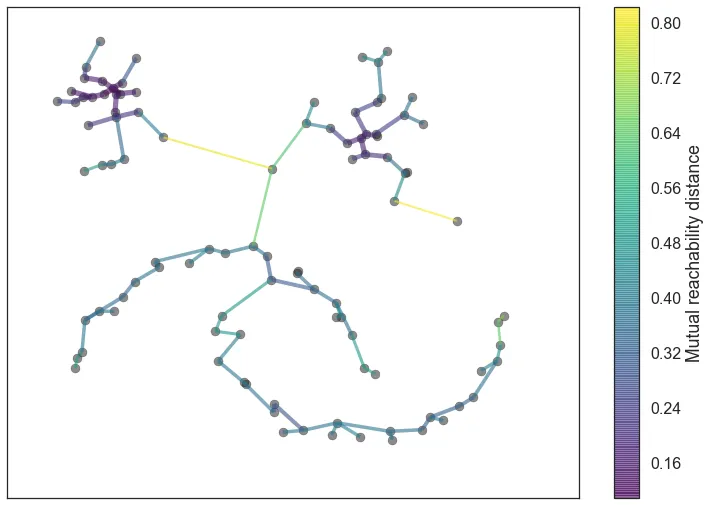
这样就得到了连接个样本点的条边,任何一条边都可以将大树分为两棵子树,可以利用它们进行层次聚类
- 初始化每一个样本点为一个初始簇
- 取出长度最小的边,将两端的两个簇合并
- 重复1,直到所有边都取出
这样,就得到了一颗聚类树(图源hdbscan.readthedocs.io)
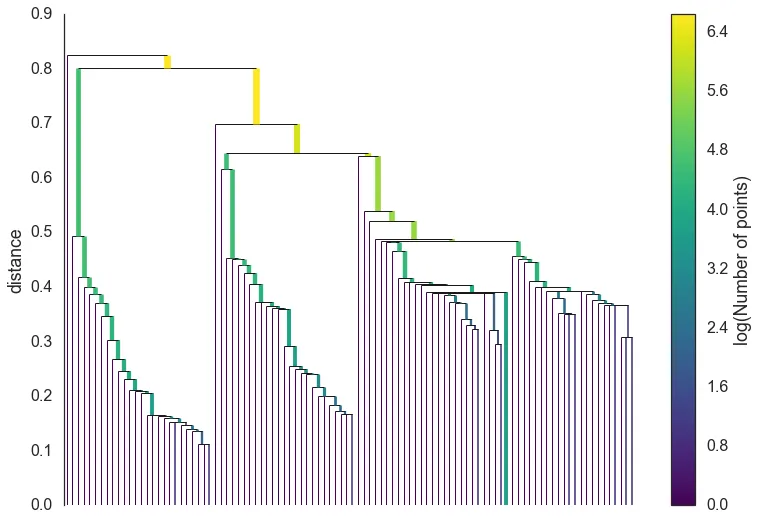
图中每一个节点的高度代表合并它两个子簇的最小生成树的边的长度,它下面竖条的颜色代表它含有的样本点数目
稳定度与类选择
为了噪声过滤与选择类,定义一个参数:最小簇大小,不妨将其记为m。进行如下的噪声过滤过程
- 初始考察根节点
- 若当前节点所含的样本数目小于最小簇大小,将其标记为噪声,不再递归考察子节点,返回
- 若当前节点的两个子节点存在一个小于最小簇大小,则将小的那个标记为噪声,考察大的子节点
- 若两个子节点都大于最小簇大小,分别再考察两个子节点
这一步排除了所有的小簇,下一步是分配类标签
- 为根节点分配类标签,考察根节点
- 若当前节点是噪声,则认为它从属的类在此时消亡,不再递归考察,返回
- 若两个子节点都不是噪声,则认为分裂有效,为两个子节点分别分配新的类标签,并考察两个子节点。认为当前节点从属的类在此时消亡,两个新的类在此时诞生
- 若两个子节点存在一个是噪声,则另一个子节点继承当前节点的类标签,递归考察它
做完这一步后,就从聚类树得到了一颗类树(图源hdbscan.readthedocs.io)

从根类开始,类不断分裂为两个子类,直到消亡。至于左侧的 是什么,这就需要定义生命周期
定义一个聚类树中节点值为
其中是层级聚类过程中合并产生该节点的边的长度。可以看作时间,增大的过程看作是时间的演化。那么类树的分裂就可以看作是:随着时间的演化,不断有样本从大类中剥离,大类不断分裂为子类。由此定义类的生命周期
- : 父类分裂诞生两个新类,分裂处节点的 值
- : 类消亡,消亡处节点的 值
对于一个类,对于它的包含的某个样本,可以定义:在某个节点处,样本被剥离出父类,该节点的值即为
随后,对于任意类,可以计算它的稳定度
直观上来看,一个类的稳定度就是类树中它下面的那一长条的面积。自然,稳定度越大的类是越好的,所以有这样的类选择规则
类选择规则
将所有叶子类设置为选择,自下而上地考察父类
- 若父类的稳定度小于两个子类的稳定度之和,那么不选择父类,并把父类的稳定度设置为两个子类的稳定度之和
- 若父类的稳定度大于两个子类的稳定度之和,则将父类设置为选择,将所有的子类设置为不选择
这样,就从类树中选择了一系列的类(图源hdbscan.readthedocs.io)
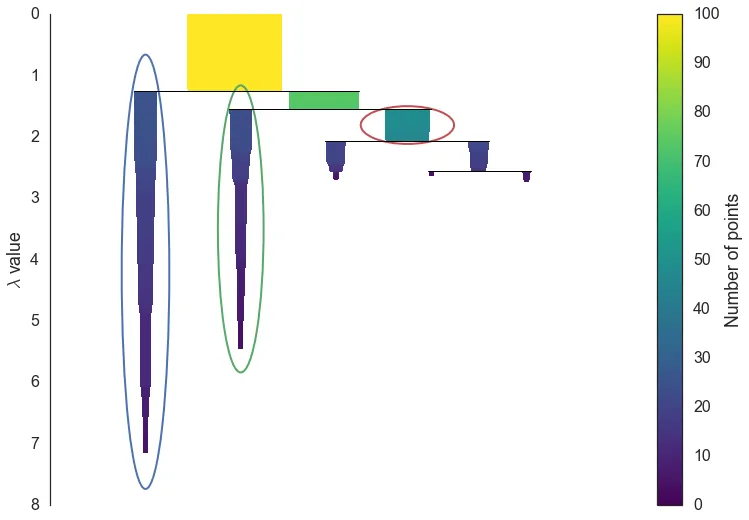
最终的聚类结构就是(图源hdbscan.readthedocs.io)
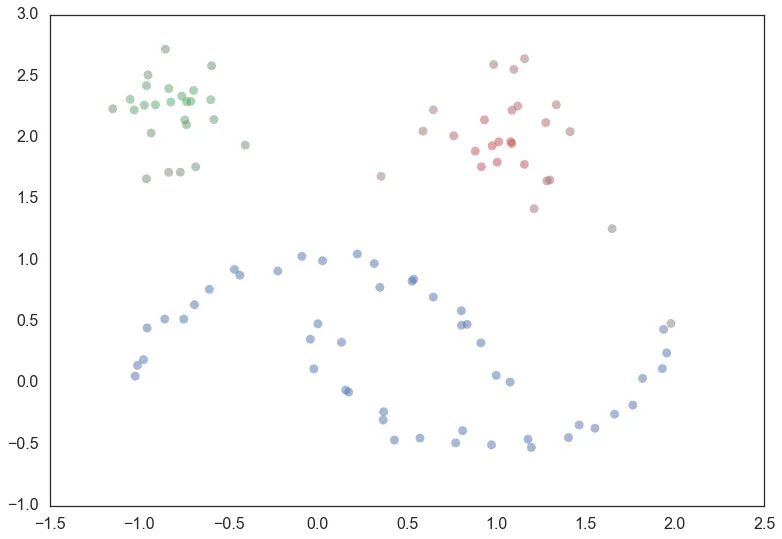
本文作者:GBwater
本文链接:
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!