施密特触发器
施密特触发器由两个CMOS反相器串联组成,通过两个电阻将输出端的电压反馈到第一个反相器的输入端
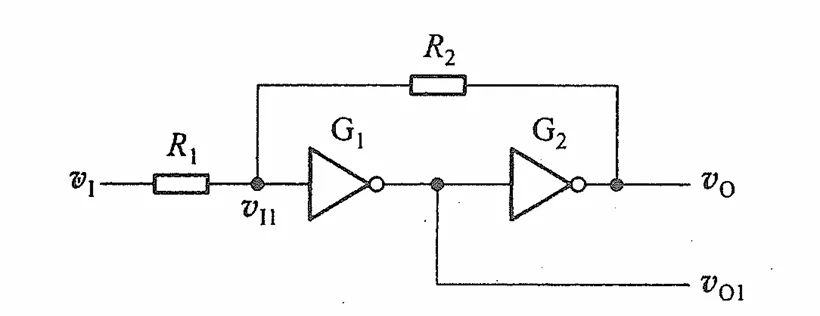
鉴于CMOS反相器没有输入电流,那么三个电压间就有关系
vI1=R1+R2R2⋅vI+R1+R2R1⋅vO
当vI逐渐上升,略大于反相器的阈值电压VTH时,则有如下路径
- vI上升使得vI1上升
- 在阈值电压附近反相器输出变化剧烈,vI1上升引起vO1下降
- vO1作为第二个反相器的输入,它下降引起vO上升
- vO上升通过电阻R2使得vI1上升
一般而言阈值电压是高电平的一半
VTH=21VDD
这样的正反馈路径使得vO迅速跳到高电平。假定电路处于低电平状态,使得其跳到高电平的vI存在一个阈值。代入vO=0得到正向阈值电压
VT+=(1+R2R1)VTH
同样,在电路状态为高电平时,输入电压在阈值附近下降有如下路径
- vI下降使得vI1下降
- 在阈值电压附近反相器输出变化剧烈,vI1下降引起vO1上升
- vO1作为第二个反相器的输入,它上升引起vO下降
- vO下降通过电阻R2使得vI1下降
这样的正反馈路径使得输出电压迅速降为低电平。将vO=VDD代入得到负向阈值电压,鉴于VDD=2VTH,有
VT−=(1−R2R1)VTH
它们之差称为回差电压ΔVT
ΔVT=R2R1VDD
如果输出接vO则是同向输出,电路符号为
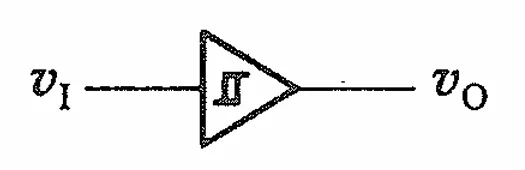
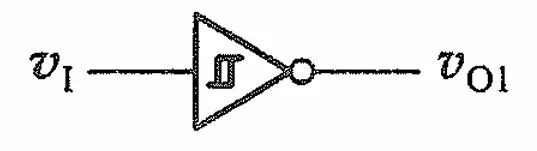
接vO1是反向输出,电路符号为
多谐振电路
只需要使得施密特触发器的输入端在高电平和低电平反复横跳,即可经过施密特触发器的整形输出震荡波形。利用一个电容可以很容易达到这一点
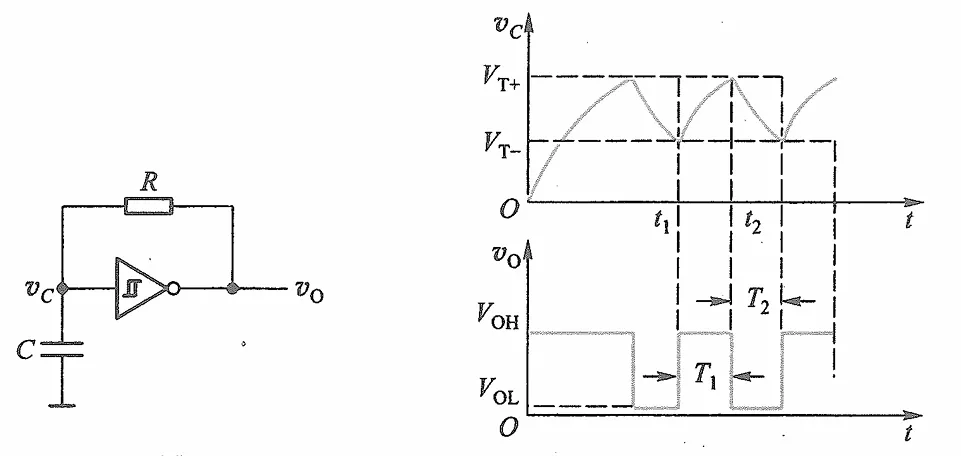
- 初始时刻电容没有充电,vC=0,vO是反相输出,为高电平
- vO经过电阻R给电容充电,使得vC逐渐上升,电压曲线符合电容的充电方程
- vC上升达到阈值VT+后,vO跳为低电平,电容放电
- vC下降达到阈值VT−后,vO跳为高电平,电容又充电,依次循环
充电电压为VDD,放电电压为0,由此给出充电时间和放电时间
T1=RClnVDD−VT+VDD−VT−,T2=RClnVT−VT+
它们之和就是周期
T=RCln(VDD−VT+VDD−VT−⋅VT−VT+)
不过这样的周期影响因素太多,不稳定,可以利用石英晶体的震荡
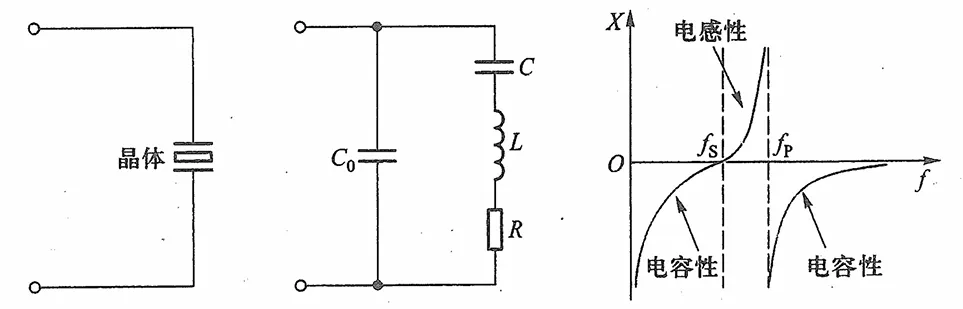
左一是石英晶体震荡电路,中间是等效电路,右边是电路的等效阻抗。若是把谐振频率选为fs,则构成串联型振荡电路,若是选在fs∼fp之间,则构成并联型振荡电路
串联型电路是这样的
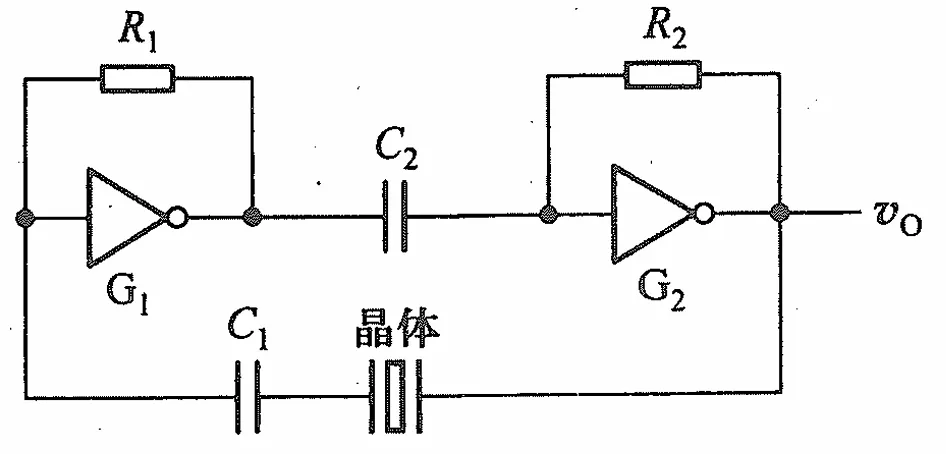
两个电阻应使得反相器工作在放大区,有利于电路起振,两个电容应使得在频率fs时其容抗很小,保证两个反相器形成正反馈
并联型电路是这样的
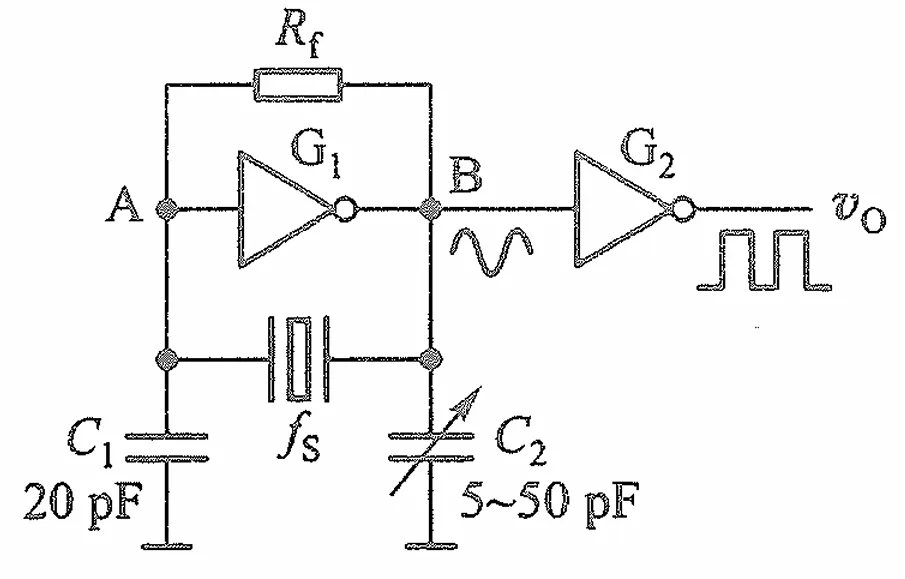
石英晶体相当于电感,与两个电容形成选频反馈电路。反相器G1工作在线性放大区,输出电压接近正弦波,由反相器G2整形为方波






