一阶马尔可夫链

某一时刻状态转移的概率只依赖前一个状态，状态之间以一定概率转移

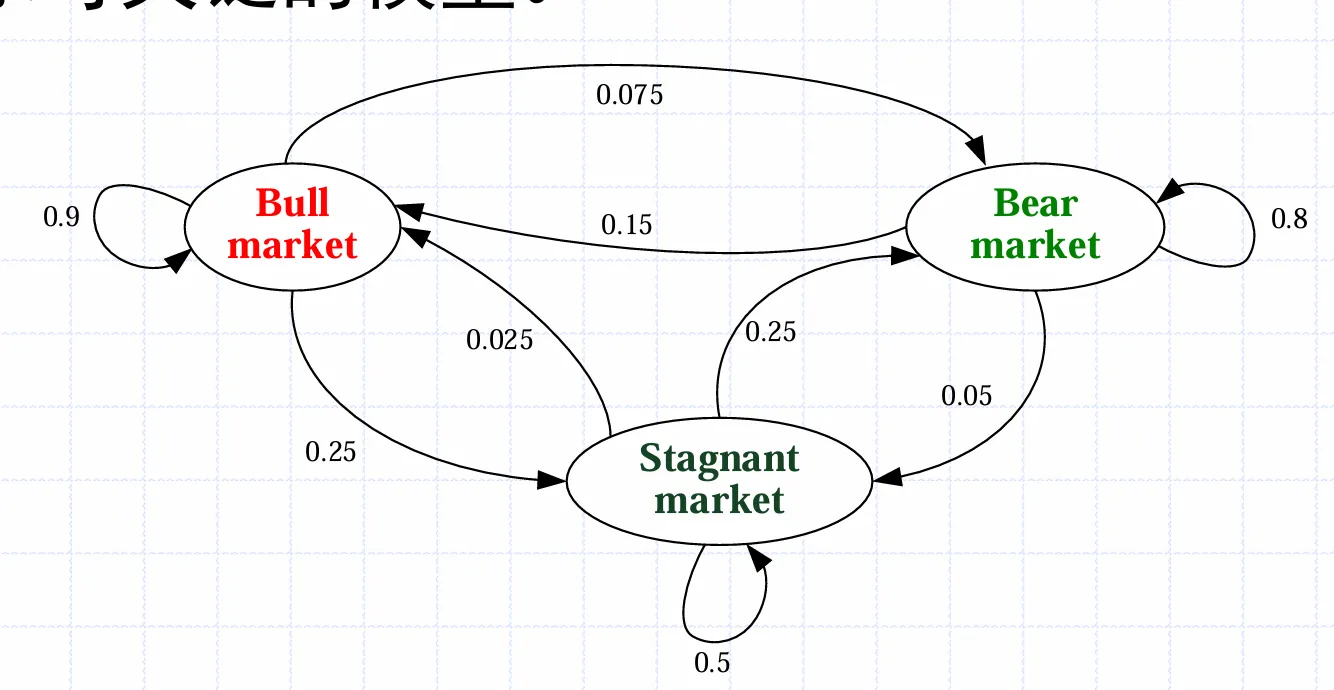
将概率写为矩阵， $P_{ij}$ 表示从状态 $i$ 转移到状态 $j$ 的概率

P=\begin{pmatrix} 0.9&0..075&0.25\\ 0.15&0.8&0.05\\ 0.025&0.25&0.5 \end{pmatrix}

$P_{ij}$ 也可以用条件概率写为

P(j|i)

那么初态也可以写完一个向量， $a_i$ 表示系统处于状态 $i$ 的概率，那么经过 $k$ 次状态转移后，系统的状态就是

P^k a

若令 $k\to\infty$ ，则状态的分布达到稳定；该稳定的状态与初态无关

隐马尔可夫模型

隐马尔可夫模型中，系统的状态不能直接观察到，只能通过传感器反映。通常来说给定状态转移模型，它只与上一刻的状态有关

P(R_t|R_{t-1})

和传感器模型，它只与当前状态有关

P(U_t|R_t)

还需要给定一个初始分布

P(R_0)

此后先根据转移模型得到转移的分布（此处是矩阵乘法）

P(R_t)=P(R_t|R_{t-1})P(R_{t-1})

然后根据传感器的结果 $u_t$ 修正分布（此处是向量的点乘）

P(R_t|u_t)=\alpha P(u_t|R_t)\cdot P(R_t)

确定性环境的决策

定义

状态的集合 $S$
每个状态下可以采取的动作集合 $A$
奖励函数 $R(s,a,s')$ ，它表示在状态 $s$ 时采取动作 $a$ 转移到状态 $s'$ 获得的奖励

可以定义效用是历史所有动作的累加，称为加性奖励

U_h(s_0,a_0,s_1,a_1,\cdots)=R(s_0,a_0,s_1)+R(s_1,a_1,s_2)+\cdots

更常用的是加性折扣奖励

U_h(s_0,a_0,s_1,a_1,\cdots)=\gamma^0R(s_0,a_0,s_1)+\gamma^1R(s_1,a_1,s_2)+\cdots

其中 $\gamma$ 称为折扣因子，接近 $0$ 时倾向于当前奖励，接近 $1$ 时倾向于长期奖励，等于 $1$ 时退化为纯加性奖励

策略就是在所有状态下应该采取的动作，最优策略是能产生最大效用的策略，它与初始状态无关

由状态 $s$ 开始执行策略 $\pi$ 的效用为

U^\pi(s)=\sum_{t=0}^\infty R(s_t,\pi(s_t),s_{t+1})

若采取加性折扣奖励，则策略 $\pi$ 的效用为

U^\pi(s)=\sum_{t=0}^\infty \gamma^t R(s_t,\pi(s_t),s_{t+1})

马尔可夫决策过程MDP

与确定性环境的决策不同的是，马尔可夫决策过程采取动作后得到的状态是随机的，由转移模型刻画。 $T(s,a,s')$ 表示采取动作 $a$ 后从状态 $s$ 转移到状态 $s'$ 的概率，即

T(s,a,s')=P(s'|s,a)

那么动作的效用也应由期望定义

U(s_0,a)=E[R(s_0,a,s_t)]=\sum_tP(s_t|s_0,a)R(s_0,a,s_t)

采用策略 $\pi$ 的效用也应该由期望定义（采样加性折扣奖励）

U^\pi(s)=E\left[\sum_{t=0}^\infty \gamma^t R(s_t,\pi(s_t),s_{t+1})\right]

效用与贝尔曼方程

一个状态的效用定义为从该状态出发的期望总奖励，正如上一节所说，从状态 $s_0$ 开始执行策略 $\pi$ 获得的期望效用为

U^\pi(s_0)=E\left[\sum_{t=0}^\infty \gamma^t R(s_t,\pi(s_t),s_{t+1})\right]

会存在一个最优的策略 $\pi^*$ ，它比其它的策略具有更大的效用

U^{\pi^*}(s)=\max(U^\pi(s))

假定已知了 $\pi^*$ 的效用为 $U(s)$ ，在状态 $s$ 下，最佳策略 $\pi^*$ 应当选取期望效用最大的动作

\pi^*(s)=\argmax_a \sum_{s'}P(s'|s,a)[R(s,a,s')+\gamma U(s')]

该动作的效用即为该状态的效用，即贝尔曼方程

Note

U(s)=\max_a \sum_{s'}P(s'|s,a)[R(s,a,s')+\gamma U(s')]

它的解就是各状态的效用

同样可以定义动作效用为给定状态下采取给定动作的期望效用

Q(s,a)= \sum_{s'}P(s'|s,a)[R(s,a,s')+\gamma U(s')]

进而写出关于动作效用的贝尔曼方程

Q(s,a)= \sum_{s'}P(s'|s,a)[R(s,a,s')+\gamma \max_{a'}Q(s',a')]

价值迭代算法

价值迭代方法是一个求解贝尔曼方程的迭代方法，可以描述如下

初始化所有效用为零
枚举每个状态，对于当前状态 $s$ ，枚举允许的所有动作，计算它们的效用

Q(s,a)= \sum_{s'}P(s'|s,a)[R(s,a,s')+\gamma U(s')]

选择具有最大效用的动作 $a$ ，用它的效用更新 $s$ 的效用

U'(s)=\max_a Q(s,a)

更新完所有状态后，令 $U=U'$ ，返回1进行下一轮迭代

价值迭代最终可以收敛于贝尔曼方程的唯一解

策略迭代算法

与价值迭代算法不同，策略迭代算法针对于策略。它可以描述如下

初始化策略 $\pi$
依据策略 $\pi$ 计算每个状态的效用（进行迭代求解）

U^\pi(s)=\sum_{s'}P(s'|s,\pi(s))[R(s,\pi(s),s')+\gamma U^\pi(s')]

基于计算得到的效用改进策略 $\pi$

\pi'(s)=\argmax_a \sum_{s'}P(s'|s,a)[R(s,a,s')+\gamma U^\pi(s')]

若改进的策略无变化，则停止迭代；否则回到1继续迭代

被动强化学习

被动强化学习指的是采取固定的策略 $\pi$ ，尝试学习效用函数 $U^\pi(S)$

一个简单的方法是直接效用估计

进行多次实验，统计每个状态的效用
对每个状态的效用进行平均，只要实验的次数足够多，均值将收敛到期望值

由于忽视了状态之间的联系，直接效用估计收敛速度较慢。解决这个问题可以使用自适应动态规划

通过反馈可以得到奖励函数
通过动作的结果可以得到转移模型
将学习到的转移模型与奖励函数代入贝尔曼方程中求解各个状态的效用

另外可以从另一个角度出发得到时序差分学习TD，它采取迭代的方式计算效用

初始化效用 $U^\pi$
学习ing：如果在状态 $s$ 下采取动作 $\pi(s)$ 达到了状态 $s'$ ，则更新 $s$ 的效用；其中 $N(s)$ 是 $s$ 出现的频率，替换概率

U^\pi(s)=U^\pi(s)+\alpha N(s)[R(s,\pi(s),s')+\gamma U^\pi(s')-U^\pi(s)]

反复执行更新操作直到收敛

TD方法调整状态的效用来达到与其观测到的后继状态一致，而自适应动态规划调整状态的效用来达到与所有可能发生的后继状态一致

TD不需要通过转移模型来进行更新

主动强化学习

可以利用策略迭代方法或者价值迭代方法求解最优策略，称为主动自适应动态规划

主动动态规划是基于贪心的，不一定收敛到最优策略，因而引入 $\epsilon-$ 贪心法，即以 $\epsilon$ 的概率尝试当前策略以外的动作，以 $1-\epsilon$ 的概率做出当前策略的动作，称其为探索与利用

探索：尝试所学习到“最优策略”以外的动作
利用：选择当前最优的动作

在选择动作时，若要进行探索，则应选取当前状态下探索次数少的动作

同样也可以推广得到主动时序差分学习，不过随着策略的更新，效用函数 $U^\pi$ 也要更新；在进行“探索”时会尝试多种策略，这意味着需要保存多个效用函数，这不好，进而将效用迭代换为动作效用的迭代

$Q(s,a)= \sum_{s'}P(s'|s,a)[R(s,a,s')+\gamma \max_{a'}Q(s',a')]$

更新规则与被动类似，同样使用频率代替转移模型

Q(s,a)=Q(s,a)+\alpha N(s)[R(s,a,s')+\gamma\max_{a'}Q(s',a')-Q(s,a)]

这种方法称为Q-learning，其中的 $Q$ 函数是最佳策略下的动作效用；与之对应的是SARSA，它使用实际采取的动作效用进行更新（不计算平均）

Q(s,a)=Q(s,a)+\alpha [R(s,a,s')+\gamma\max_{a'}Q(s',a')-Q(s,a)]

当进行探索时，若产生负面奖励，由于平均，Q-learning不会惩罚该动作，而SARSA会

Q-learning是一种离策略（off-policy）学习算法，它所学习的Q值回答了问题“假设我停止使用我正在使用的任何策略，并依照（根据估计）选择最佳动作的策略开始行动，那么这个动作在该状态下的价值是多少？”

SARSA是一种同策略（on-policy）的算法，它通过学习Q值回答了问题“假设我坚持自己的策略，那么这个动作在该状态下的价值是多少？”

目录