线性二分类

不同于回归问题，线性分类问题的标签是离散的二值

f(x)=\pm1

希望用一条直线 $y=w_1x+w_0$ 把数据分成两类，称其为决策边界

Sign(w_1x+w_0)=\pm1

可以将其推广到多变量的情形，可以如此定义一个超平面

w^Tx+b=0

一个超平面可以通过一个截距 $b$ 和一个法向量 $w$ 确定，它也称为权重向量

如果数据集可以被线性分类器分离，则称其为线性可分的

硬阈值线性分类器

回到一维情形，假定有权重， $w=(w_0,w_1)^T$ ，为了表示方便再定义 $x=(1,x)^T$ ，那么决策边界就是直线

w^Tx=0

定义一个阈值函数

Threshhold(z)= \begin{cases} 1&z\geq0\\ 0&z<0 \end{cases}

学习到的函数是

h_w(x)=Threshhold(w^Tx)

感知机是一种硬阈值线性分类器，它可以如图画出

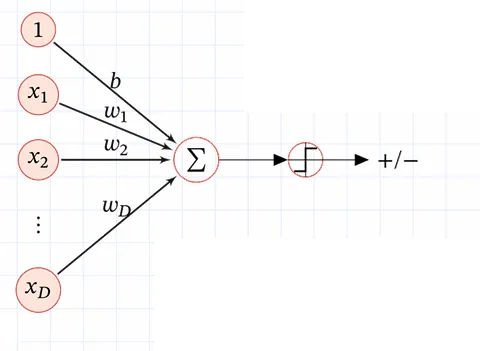
由于使用了硬阈值函数，在权重空间中几乎所有点梯度都为零，因而常规的梯度下降方法失效，需要使用权重更新算法求解

Note

w_i=w_i+\alpha(y-h_w(x))x_i

每一次更新随机选择一个样例进行学习

硬阈值线性分类器始终做出确定性的判断，不能处理边界上的样本，因而无法应对噪声数据。这可以通过引入软阈值解决

Logistic(z)=\dfrac{1}{1+e^{-z}}

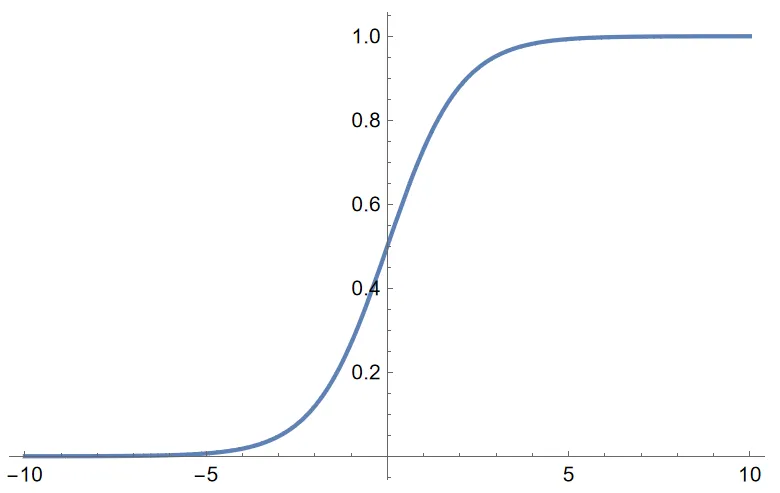
用Logistic函数代替阈值函数得到

h_w(x)=Logistic(w^Tx)