红黑树是一种自平衡的二叉搜索树，广泛应用于计算机科学中的各种领域，如操作系统的调度、数据库索引以及集合的高效管理。它通过严格的颜色规则和旋转操作，确保树的高度始终保持在较低水平，从而实现快速的插入、删除和查找操作

红黑树的定义

红黑树是一棵二叉搜索树，即树中的每个节点都应满足性质

• 左儿子比它小
• 右儿子不比它小

不过这样朴素的二叉搜索树会出现退化的问题，比如一条有序的链也是合法的二叉搜素树，此时查询的时间复杂度就会将为$O(n)$，这是不好的。为了解决这个问题，红黑树引入了染色机制

1. 每个节点都有颜色，要么为红色，要么为黑色
2. 红色节点的子节点只能为黑色
3. 每一个叶子节点视为拥有两个黑色的NULL节点
4. 每个从根到NULL的路径上具有相同数目的黑色节点

关键就在于第四条，这意味着红黑树有一条非常好的性质

这是说红黑树可以看作是“近似平衡”的二叉树，查询操作的时间复杂度上限为$O(2\log N)$。为了简单起见还规定

• 红黑树的根节点是黑色的

左旋和右旋

不同于平衡二叉树，红黑树的节点仅有两种基本操作：左旋和右旋

右旋是将节点变为左儿子的右节点

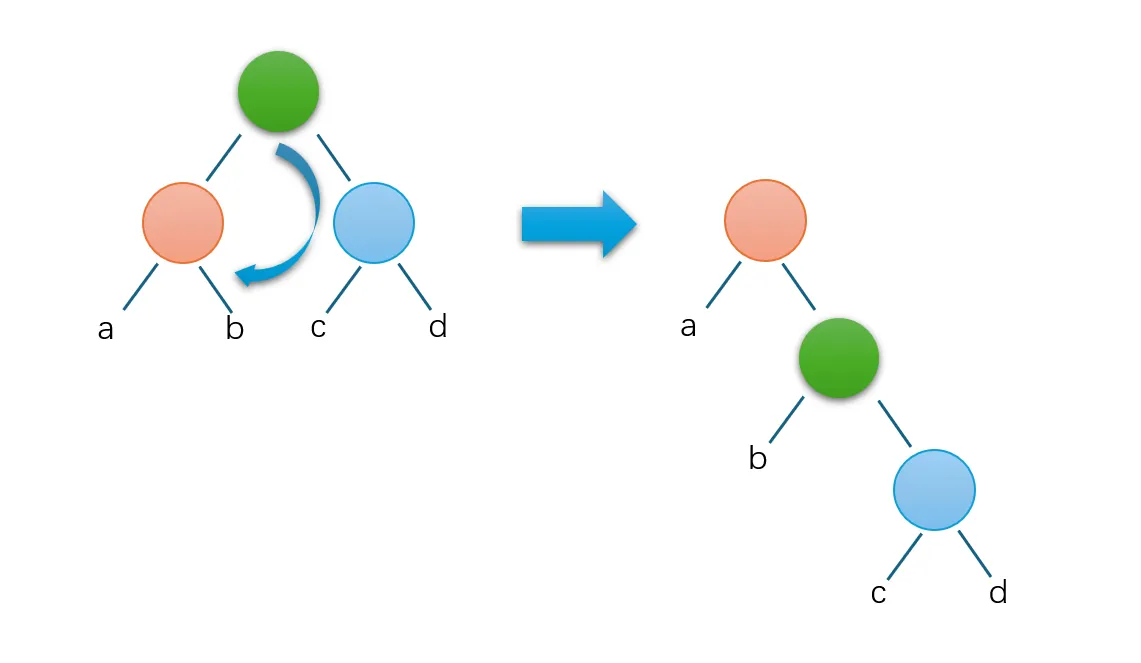
与之相反，左旋就是将节点变为右儿子的左节点

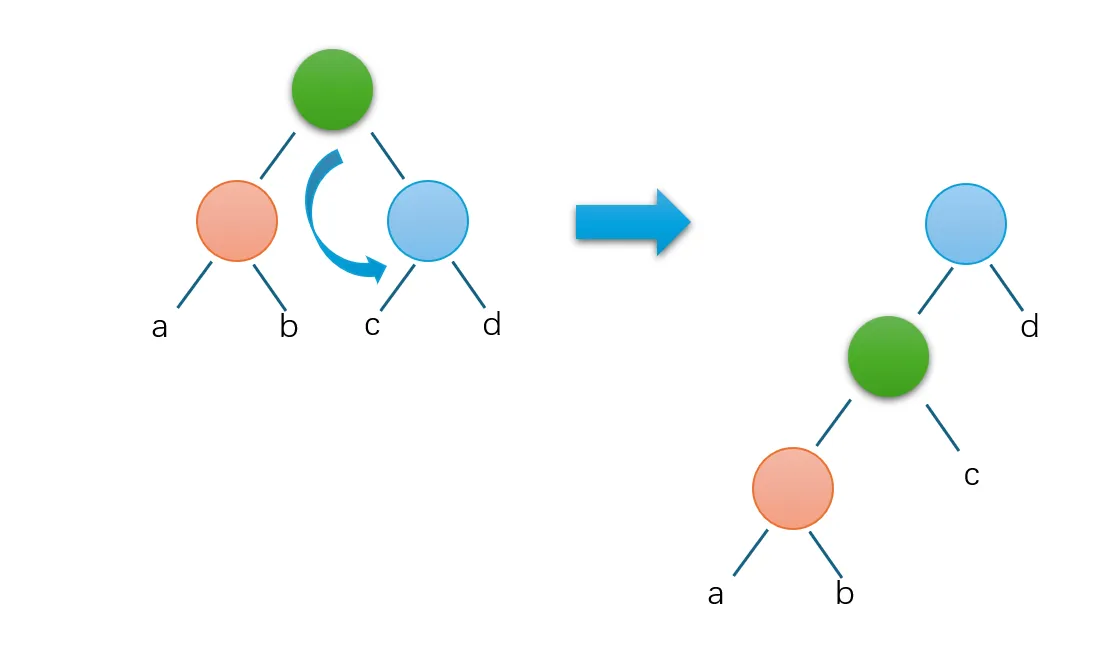
红黑树的插入

红黑树的插入分为两步

1. 按照二叉搜索树的方式插入
2. 根据染色规则调整树的结构并重新染色

插入的节点会成为叶子，由于需要保持黑高度，将其设为红色。不过这样可能会导致违规，即红色节点不能有红色的儿子。可以分为三种情况递归地调整颜色

0. 若该节点的父亲为黑色

这很好，不需要做调整

1. 父亲为红色，并且父亲是爷爷的左儿子，而且父亲的兄弟也是红的

这种情况可以如图处理

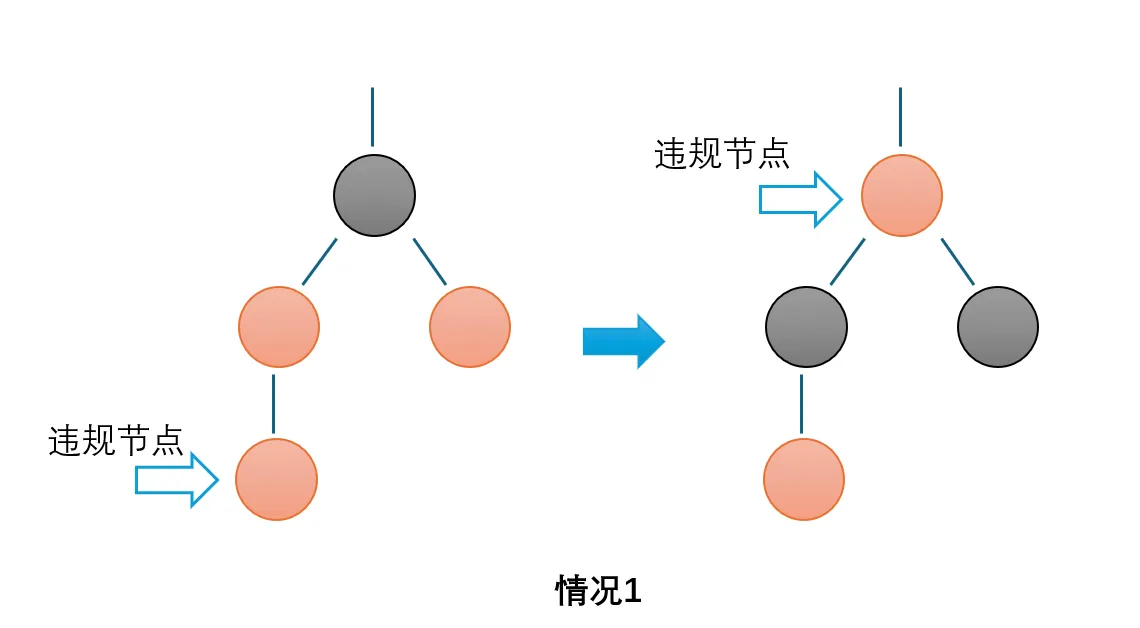
将爷爷设置为红色，再将父亲和父亲的兄弟设置为黑色即可。然后递归处理爷爷即可

2. 父亲为红色，并且父亲是爷爷的左儿子，不过父亲的兄弟是黑的，同时自己是父亲的右儿子

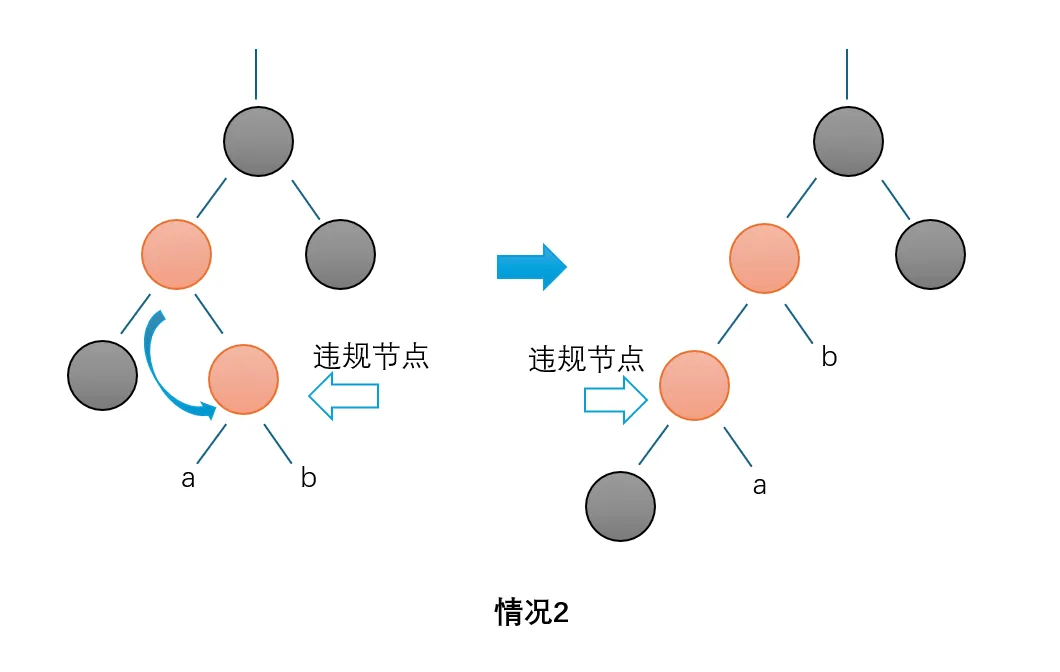
对父亲执行左旋操作，再递归处理即可

3. 父亲为红色，并且父亲是爷爷的左儿子，不过父亲的兄弟是黑的，同时自己是父亲的左儿子

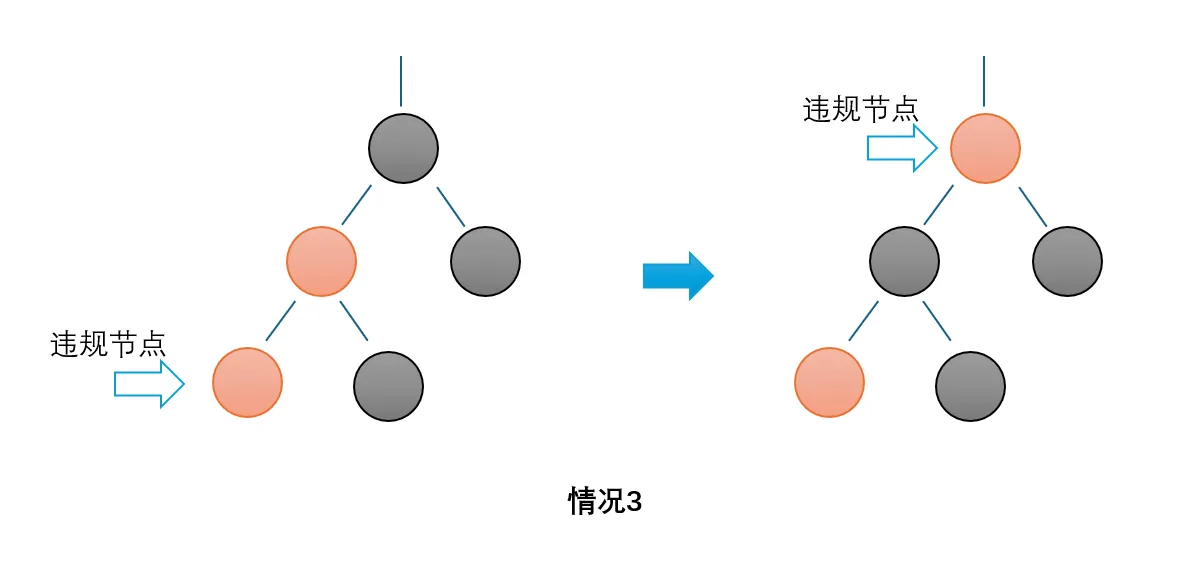
将父亲设为黑色，将爷爷设置为红色，再递归处理爷爷即可

---

对于父亲是爷爷右儿子的情况，操作是相同的，只是需要将左旋操作改为右旋即可

这就是所有可能出现的情况，这些操作都保持每个节点的黑高度不变，每次操作使得违规节点上升一层，那么调整的时间复杂度为$O(\log N)$

红黑树的删除

由于朴素的二叉搜索树执行删除操作时是先替换再删除，即若删除某个非叶子节点

1. 将该节点的值与左子树的最大值或是右子树的最小值交换一下（只换值不换颜色！），注意它们不一定是叶子节点
2. 删除交换后的节点

若默认要删除的节点是它父亲的左儿子，可以分为三种情况

1. 要删除的节点是叶子节点

删除一个红色的叶子不需要做任何额外的操作，删除一个黑色的叶子就不一样了。为了保持黑高度，需要假定删除后会在原位留下一个双重黑的NULL节点，意为该路径上黑高度+1

2. 要删除的节点仅有一个儿子

删除仅有一个儿子的红节点只需要用它的儿子替换它即可，不需要额外操作。

不过如果它是黑的，由于一棵子树是空的，那么非空的子树高度必定为1，意味着它的儿子只能是一个红色的叶子。此时将它替换为儿子后为了保持黑高度，儿子应当变黑。为了方便操作，记它是红黑的，代表它是红的但应当变黑

3. 要删除的节点有两个儿子

按照惯例此时应当在右子树寻找最小的节点，该节点必定不存在左儿子（因为没有比它更小的了）。将它的值与待删除的节点交换后即转化为情形二

---

那么要解决的就是双重黑和红黑的节点，需要将它变为单重黑或者单纯的红色。无论是双重黑还是红黑，本质上都是对一个节点加了一层黑，实现该操作即可

0. 它是红的

将它变黑即可。由于将一个红节点变黑并不会违背红黑树的性质，因而此时的红黑树已经合规，结束

1. 它是黑的，但它的兄弟是红的

这意味着它的父亲一定是黑的，可以如图操作

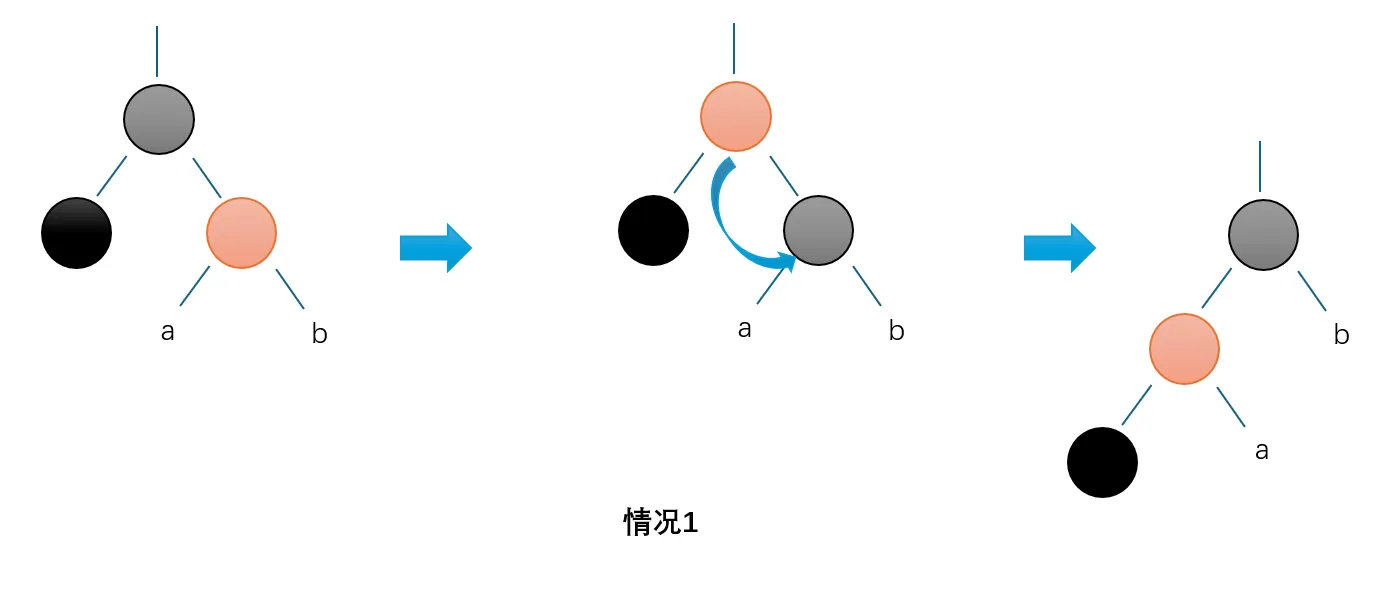
这样操作后可以保证a，b子树和双重黑子树的黑高度不变，同时将双重黑节点的父亲变为了红色

2. 它是黑的，它的兄弟也是黑的，并且兄弟的两个儿子也是黑的

既然它和兄弟都是黑的，它们俩都脱去一层黑，并对父亲加黑即可。即将一层黑色送给了父亲

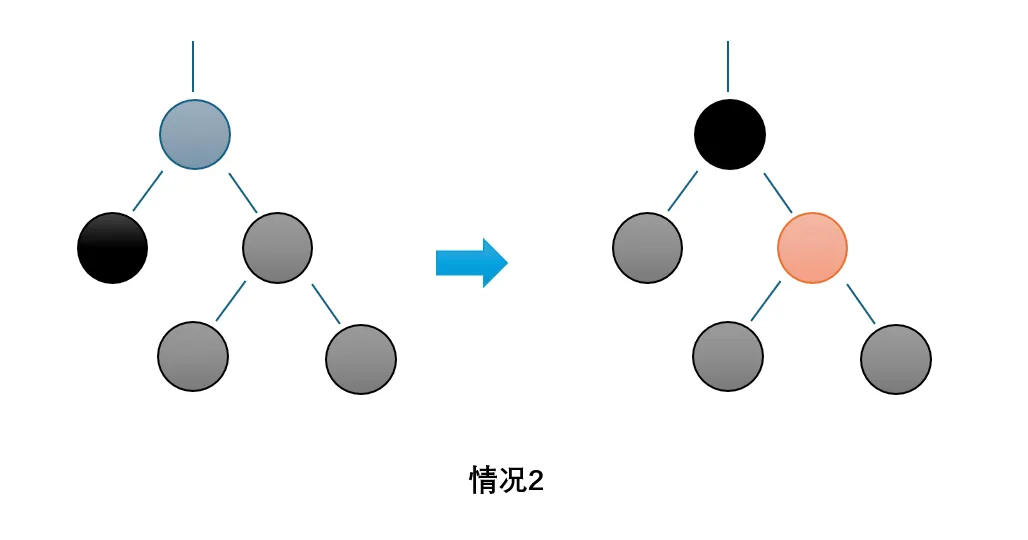
3. 它是黑的，它的兄弟是黑的，但是兄弟的左儿子是红的，右儿子是黑的

那么将兄弟和它的左儿子交换颜色，然后对兄弟节点执行右旋操作

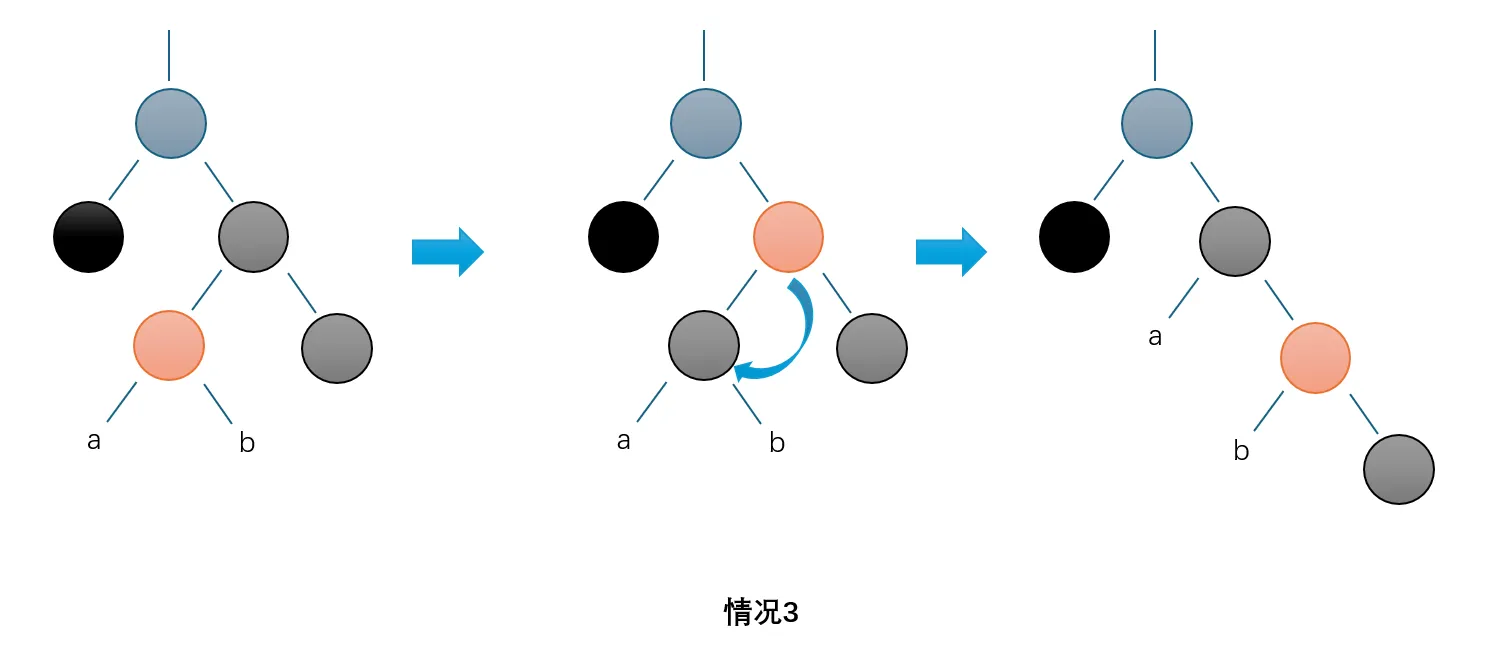
这样就变为右儿子是红色的情况

4. 它是黑的，它的兄弟是黑的，但是兄弟的右儿子是红的，左儿子不知道是什么颜色

兄弟的颜色与父亲的颜色互换，再对父亲执行左旋操作

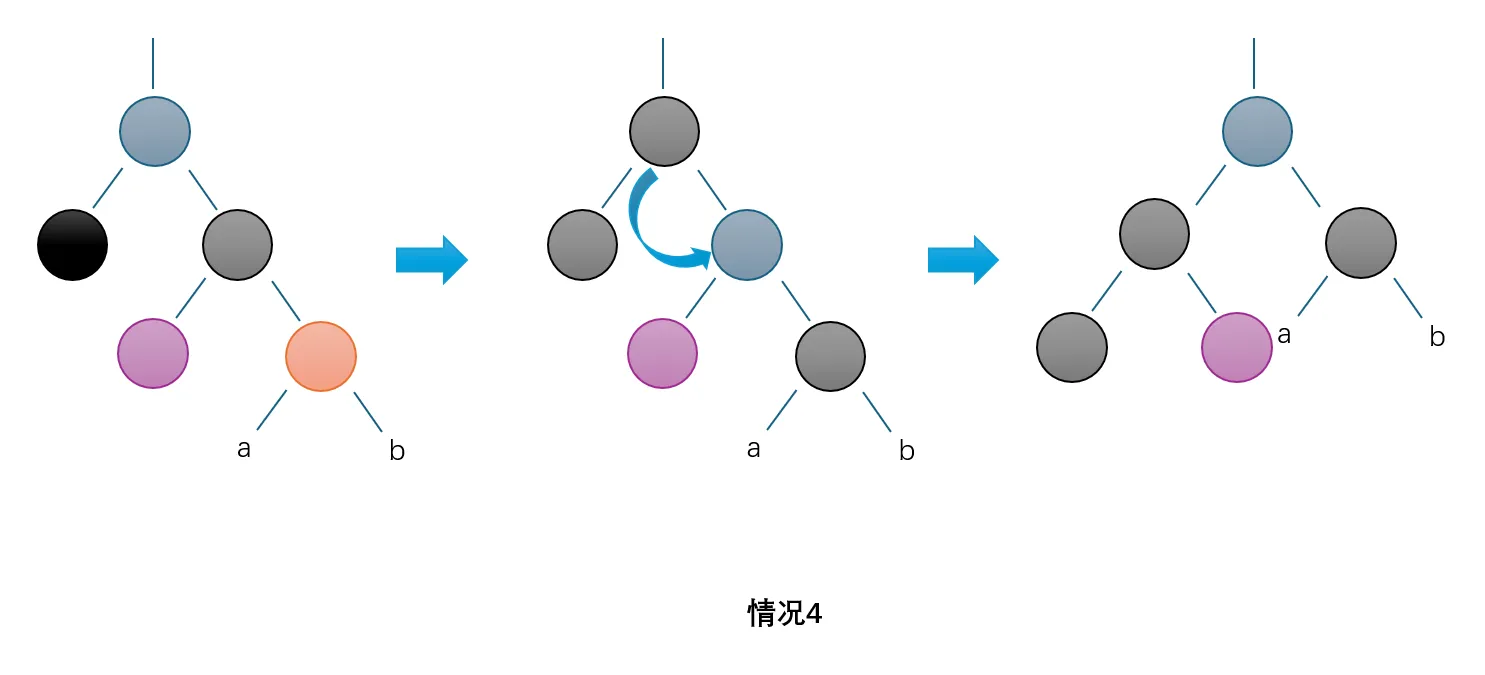
这样它的黑高度变为了父亲+2，其余节点的黑高度均维持不变。同时父亲的颜色不变，因而现在已经合规，不需要再调整，结束即可

---

上面是对于左儿子的加黑操作，对于右儿子的加黑操作对称即可

简单C++红黑树类实现

为了算法课的作业 可以简单地实现一个红黑树rbtree.h，简单起见就用指针实现了，如果放在OI中应该用数组实现码量会小一些 不过正经人谁在OI里写红黑树啊

都用C++了，不写成类怎么体现出C艹的优雅，就酱吧。不过老师要求输出中序遍历，还是加上了string.h的头文件，有点可惜

cpp
#include <string>
class rbtree
{
private:
    // 红黑树的节点类
    class node
    {
    public:
        int data;
        node *left;
        node *right;
        node *parent;
        int color; // 0为黑色，1为红色

        node(int data)
        {
            this->data = data;
            left = right = parent = NULL;
            color = 1; // 新插入节点默认为红色
        }
    };
    node *root;

    // 左旋
    void rotateLeft(node *&root, node *&pt)
    {
        node *pt_right = pt->right;
        pt->right = pt_right->left;

        if (pt->right != NULL)
            pt->right->parent = pt;

        pt_right->parent = pt->parent;

        if (pt->parent == NULL)
            root = pt_right;
        else if (pt == pt->parent->left)
            pt->parent->left = pt_right;
        else
            pt->parent->right = pt_right;

        pt_right->left = pt;
        pt->parent = pt_right;
    }
    // 右旋
    void rotateRight(node *&root, node *&pt)
    {
        node *pt_left = pt->left;
        pt->left = pt_left->right;

        if (pt->left != NULL)
            pt->left->parent = pt;

        pt_left->parent = pt->parent;

        if (pt->parent == NULL)
            root = pt_left;
        else if (pt == pt->parent->left)
            pt->parent->left = pt_left;
        else
            pt->parent->right = pt_left;

        pt_left->right = pt;
        pt->parent = pt_left;
    }
    // 修正红黑树性质
    void fixViolation(node *&root, node *&pt)
    {
        node *parent_pt = NULL;
        node *grand_parent_pt = NULL;

        while ((pt != root) && (pt->color == 1) &&
               (pt->parent->color == 1))
        {
            parent_pt = pt->parent;
            grand_parent_pt = parent_pt->parent;

            /* 情况A: 父节点是祖父节点的左孩子 */
            if (parent_pt == grand_parent_pt->left)
            {
                node *uncle_pt = grand_parent_pt->right;

                /* 情况1:
                   叔叔节点是红色，只需要重新上色和向上合并 */
                if (uncle_pt != NULL && uncle_pt->color == 1)
                {
                    grand_parent_pt->color = 1;
                    parent_pt->color = 0;
                    uncle_pt->color = 0;
                    pt = grand_parent_pt;
                }

                else
                {
                    /* 情况2:
                       pt是父节点的右孩子，先左旋转父节点 */
                    if (pt == parent_pt->right)
                    {
                        rotateLeft(root, parent_pt);
                        pt = parent_pt;
                        parent_pt = pt->parent;
                    }

                    /* 情况3:
                       pt是父节点的左孩子，对祖父节点右旋并调整颜色 */
                    rotateRight(root, grand_parent_pt);
                    int t = parent_pt->color;
                    parent_pt->color = grand_parent_pt->color;
                    grand_parent_pt->color = t;
                    pt = parent_pt;
                }
            }

            /* 情况B: 父节点是祖父节点的右孩子 */
            else
            {
                node *uncle_pt = grand_parent_pt->left;

                /* 情况1:
                   叔叔节点是红色 */
                if ((uncle_pt != NULL) && (uncle_pt->color == 1))
                {
                    grand_parent_pt->color = 1;
                    parent_pt->color = 0;
                    uncle_pt->color = 0;
                    pt = grand_parent_pt;
                }
                else
                {
                    /* 情况2:
                       pt是父节点的左孩子，先右旋父节点 */
                    if (pt == parent_pt->left)
                    {
                        rotateRight(root, parent_pt);
                        pt = parent_pt;
                        parent_pt = pt->parent;
                    }

                    /* 情况3:
                       pt是父节点的右孩子，对祖父节点左旋并调整颜色 */
                    rotateLeft(root, grand_parent_pt);
                    int t = parent_pt->color;
                    parent_pt->color = grand_parent_pt->color;
                    grand_parent_pt->color = t;
                    pt = parent_pt;
                }
            }
        }

        root->color = 0;
    }

    // 删除整棵树
    void deleteTree(node *root)
    {
        if (root == NULL)
            return;
        deleteTree(root->left);
        deleteTree(root->right);
        delete root;
    }

    // 寻找最小值节点（用于找后继）
    node *minimum(node *x)
    {
        while (x->left != NULL)
            x = x->left;
        return x;
    }

    // 用v子树替换u子树
    void rbTransplant(node *&root, node *u, node *v)
    {
        if (u->parent == NULL)
            root = v;
        else if (u == u->parent->left)
            u->parent->left = v;
        else
            u->parent->right = v;
        if (v != NULL)
            v->parent = u->parent;
    }

    // 删除修正函数
    void fixDelete(node *&root, node *x)
    {
        while (x != root && (x == NULL || x->color == 0))
        {
            if (x == x->parent->left)
            {
                node *w = x->parent->right;
                if (w != NULL && w->color == 1)
                {
                    w->color = 0;
                    x->parent->color = 1;
                    rotateLeft(root, x->parent);
                    w = x->parent->right;
                }
                if ((w->left == NULL || w->left->color == 0) &&
                    (w->right == NULL || w->right->color == 0))
                {
                    w->color = 1;
                    x = x->parent;
                }
                else
                {
                    if (w->right == NULL || w->right->color == 0)
                    {
                        if (w->left != NULL)
                            w->left->color = 0;
                        w->color = 1;
                        rotateRight(root, w);
                        w = x->parent->right;
                    }
                    w->color = x->parent->color;
                    x->parent->color = 0;
                    if (w->right != NULL)
                        w->right->color = 0;
                    rotateLeft(root, x->parent);
                    x = root;
                }
            }
            else
            {
                node *w = x->parent->left;
                if (w != NULL && w->color == 1)
                {
                    w->color = 0;
                    x->parent->color = 1;
                    rotateRight(root, x->parent);
                    w = x->parent->left;
                }
                if ((w->right == NULL || w->right->color == 0) &&
                    (w->left == NULL || w->left->color == 0))
                {
                    w->color = 1;
                    x = x->parent;
                }
                else
                {
                    if (w->left == NULL || w->left->color == 0)
                    {
                        if (w->right != NULL)
                            w->right->color = 0;
                        w->color = 1;
                        rotateLeft(root, w);
                        w = x->parent->left;
                    }
                    w->color = x->parent->color;
                    x->parent->color = 0;
                    if (w->left != NULL)
                        w->left->color = 0;
                    rotateRight(root, x->parent);
                    x = root;
                }
            }
        }
        if (x != NULL)
            x->color = 0;
    }

    // 寻找键值为key的节点
    node *searchNode(node *root, int key)
    {
        if (root == NULL || root->data == key)
            return root;
        if (key < root->data)
            return searchNode(root->left, key);
        return searchNode(root->right, key);
    }

public:
    rbtree()
    {
        root = NULL;
    }

    ~rbtree()
    {
        deleteTree(root);
    }

    // 插入键为data的节点
    void insert(const int &data)
    {
        node *pt = new node(data);

        // 普通的二叉搜索树插入
        if (root == NULL)
        {
            root = pt;
            root->color = 0; // 根节点为黑色
            return;
        }
        else
        {
            node *parent = NULL;
            node *current = root;

            while (current != NULL)
            {
                parent = current;
                if (pt->data < current->data)
                    current = current->left;
                else
                    current = current->right;
            }

            pt->parent = parent;
            if (pt->data < parent->data)
                parent->left = pt;
            else
                parent->right = pt;
        }

        // 修正红黑树性质
        fixViolation(root, pt);
    }

    // 删除键为key的节点
    void deleteKey(int key)
    {
        node *z = searchNode(root, key);
        if (z == NULL)
            return; // 未找到要删除的节点，直接返回

        node *y = z;
        node *x = NULL;
        int y_original_color = y->color;

        // 若被删节点z只有一个子节点或无子节点
        if (z->left == NULL)
        {
            x = z->right;
            rbTransplant(root, z, z->right);
        }
        else if (z->right == NULL)
        {
            x = z->left;
            rbTransplant(root, z, z->left);
        }
        else
        {
            // 若被删节点有两个子节点，则用后继替换
            y = minimum(z->right);
            y_original_color = y->color;
            x = y->right;
            if (y->parent == z)
            {
                if (x != NULL)
                    x->parent = y;
            }
            else
            {
                rbTransplant(root, y, y->right);
                y->right = z->right;
                if (y->right != NULL)
                    y->right->parent = y;
            }
            rbTransplant(root, z, y);
            y->left = z->left;
            y->left->parent = y;
            y->color = z->color;
        }

        delete z;

        // 如果被删除的颜色是黑色，需要修正
        if (y_original_color == 0 && x != NULL)
            fixDelete(root, x);
    }

    // 返回以root为根的中序遍历
    std::string inorder(node *root)
    {
        if (root == NULL)
            return std::string("");
        std::string instr = inorder(root->left);
        instr += std::to_string(root->data) + "(" + (root->color == 0 ? "B" : "R") + ") ";
        instr += inorder(root->right);
        return instr;
    }

    // 中序遍历
    std::string inorder()
    {
        return inorder(root);
    }
};