感谢秦晓卫老师的指导！！

局部搜索

在大规模问题中没有足够内存去存储整个边界集合，并且很多实际问题只关注最终状态，不关心到达路径，即局部搜索。它可表征为求解最优化问题，根据目标函数找到最优状态

爬山

爬山算法的策略可以概述为

因此爬山算法只能找到局部最优而无法找到全局最优，它具有以下几个问题

局部极大值

爬山算法停留在某个局部的“山头”，但是存在更高的山头

平台区

爬山算法进行到平台区时，相邻的节点代价都相等，无法继续前进

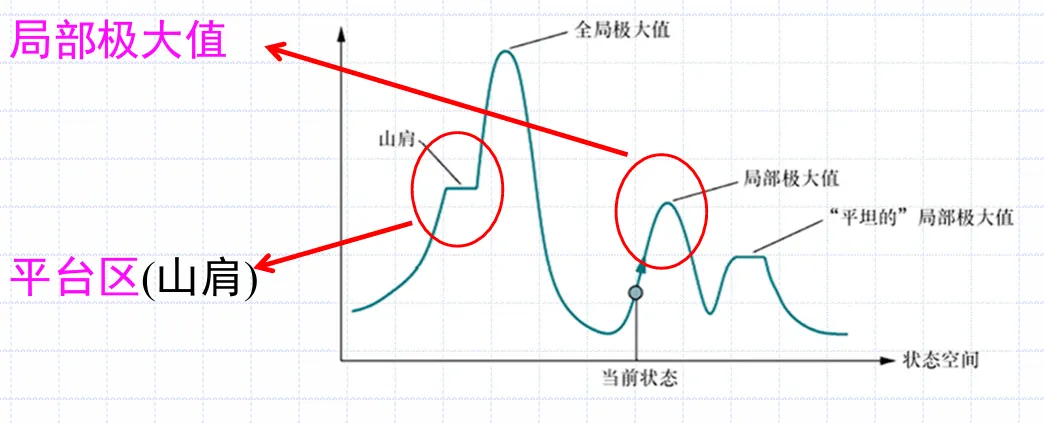
岭

若在局部存在多个节点，它们都比相邻的节点更优，但是它们之间不能转移。爬山算法会停留在它们之中的一个

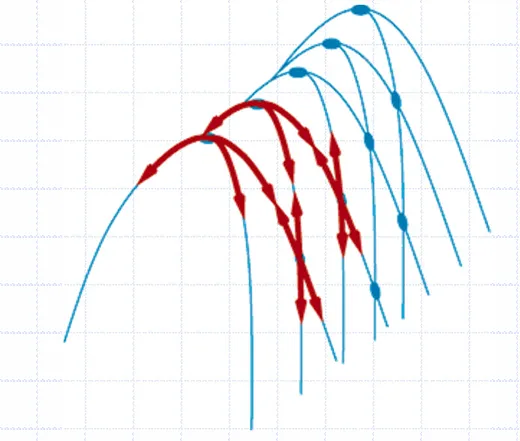
为了解决这个问题，有如下的改进方案

1. 允许横向移动：可以越过平台区
2. 随机爬山法: 在上坡行动中按按概率随机选择一个
3. 首选爬山法: 不断随机生成后继，如果遇到比当前状态好的后继就选择
4. 随机重启爬山法: 反复随机生成初始状态执行爬山法，直到实现目标

但是不论是何种改进，都无法从根本上解决不完备的问题

模拟退火

模拟退火综合了爬山法和随机游走法

• 爬山法: 从不下坡, 高效但不完备
• 随机游走法: 不考虑状态值随机移动, 效率低但完备

模拟退火法模拟了退火的过程。其核心是定义了一个随时间逐渐下降的温度$T$，在状态转移的过程中，如果后继的状态比当前的状态差，则以一定概率选择

综合来说，状态转移被接受的概率为

模拟退火法允许了下山的过程，能跨过“势垒”，从而有机会找到全局最优解

最大化收益的模拟退火算法可以描述如下

0. 初始化：给定初始状态，初始温度
1. 以特定方案降低温度，若温度$T=0$，则返回当前状态作为解
2. 选择一个后继状态，计算收益差$\Delta E=Value(当前)-Value(后继)$
3. 若$\Delta E<0$，即后继收益更大，则选择后继替换当前；若$\Delta E>0$,则以概率$e^{-\Delta E}$接受
4. 返回1循环