感谢秦晓卫老师的指导！！

有信息搜索

有信息(启发式)搜索:在问题提供的定义之外, 还可利用关于目标状态的特定领域线索

线索以启发式函数(Heuristic Function)的形式出现, 记为 $h(n)$

贪心最佳优先搜索

一个启发式函数的例子为

Note

$h(n)$ =从节点n的状态到目标状态的最小代价路径的估计值

朴素的启发式搜索采取贪心的方式，即取评价函数为 $h(n)$ ，这样每次会优先扩展使得启发式函数最小的节点。但是 $h(n)$ 并不能保证正确性，会出现“朝着错误目标一路狂奔”的现象

A*搜索综合了UCS和贪心方案，取评价函数为

f(n)=g(n)+h(n)

其中 $g(n)$ 是初始状态到节点n的路径代价， $h(n)$ 为节点n到目标状态的最短路径的代价估计值

定义 可容许性(admissible)启发式函数

可容许性启发式函数

函数永远不会高估某个目标的代价

一个可容许性启发式函数的例子是，若代价是空间的路径长度，那么

h(n)=直线距离

小于等于所有可能路径长度，是一个可容许性启发式函数。有定理

A*搜索的最优性

如果A搜索策略的启发式函数h(n)是可容许性的, 则A搜索策略一定是最优的

可以利用反证法证明。假定最优路径代价为 $C^*$ ，但是算法返回了 $C>C^*$ ，这意味着算法没有扩展出最优路径，也就是说最优路径上有节点没有被扩展到，记该节点为n

由于算法返回了代价 $C$ ，所有代价小于 $C$ 的节点都被扩展过了，也就是说

f(n)>C\Leftrightarrow g(n)+h(n)>C

由于节点n在最优路径上， $g(n)$ 应当是最小的路径代价，那么

f(n)=g^*(n)+h(n)

记真实的代价函数为 $h^*(n)$ ，由于 $h(n)$ 是可容许的，即 $h(n)\leq h^*(n)$ ，那么

f(n)\leq g^*(n)+h^*(n)

而最优路径代价正是 $C^*=g^*(n)+h^*(n)$ ，这意味着

f(n)\leq C^*

而一开始有

f(n)> C>C^*

这是矛盾的，因而假设不成立。Q.E.D

定义 一致性(consistency)启发式函数

一致性启发式函数

每个 $n$ 以及由动作a生成的n的每个后继节点 $n’$ 均满足条件

h(n)\leq c(n,a,n')+h(n')

其中 $c(n,a,n')$ 是从 $n$ 以动作a转移到 $n'$ 的代价，可以参照示意图

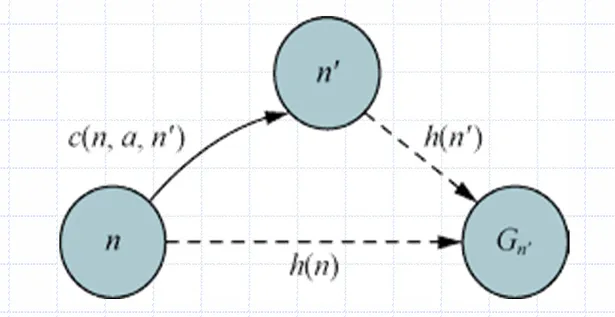
即 $h(n)$ 满足“三角形两边之和大于第三边”的性质。有定理

A*搜索的最优性

若搜索策略的启发式函数 $h(n)$ 是一致性的, 则A*搜索策略一定是最优的

原问题去除部分约束获得问题称为松弛问题

Note

一个松弛问题的最优解的代价函数是原问题的可容许性启发式函数

这是因为松弛问题的最优解的代价总小于原问题的最优解。如下面这个问题

将将三角形挪到圆形位置，黑色方框为障碍物。考虑松弛问题，去除障碍物，此时的最优解代价就是 曼哈顿距离